in Elettronica |

Tecniche di progettazione IIR: Varianza Impulsiva – Ulteriori considerazioni

In questo articolo andremo a trattare alcune ulteriori considerazioni su una delle tecniche di progettazione di filtri IIR, ovvero il metodo della varianza impulsiva.

Nel precedente articolo abbiamo definito il metodo, derivandone l’espressione matematica e definendo alcuni vincoli progettuali a cui bisogna attenersi per questa tipologia di filtri.

Consideriamo ora la risposta impulsiva nel tempo:

{ h }_{ a }(t)=\frac { 1 }{ \alpha } { e }^{ -\frac { t }{ \alpha } }u(t)

Si ricava la risposta impulsiva h[n] a tempo discreto:

h[n]=T\cdot { h }_{ a }(nT)

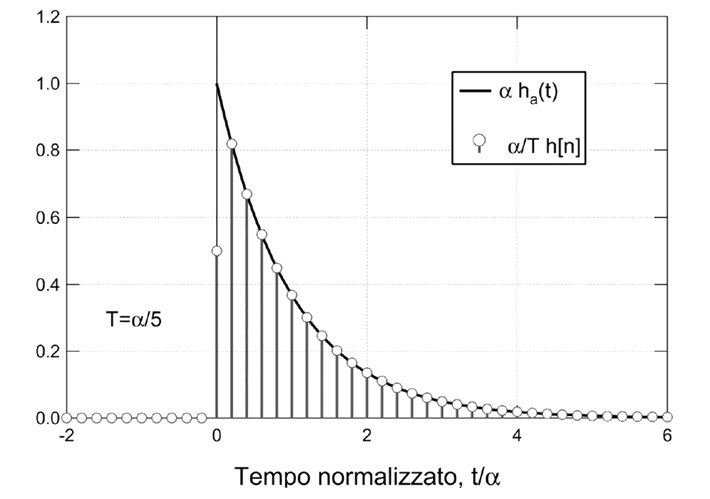
In questo modo si andrà incontro ad una ambiguità in t=0, perchè ha(t) è discontinua. Risulta necessario trovare un valore intermedio valido tra 0+ e 0–.

Tale valore viene individuato come la semisomma dei limiti destro e sinistro:

\begin{cases} h({ 0 }^{ – })=0 \\ h({ 0 }^{ + })=\sum _{ i=1 }^{ N }{ { A }_{ i } } \end{cases}\quad \Rightarrow \quad h[0]=\frac { T }{ 2 } \left( h({ 0 }^{ + })+h({ 0 }^{ – }) \right) =\frac { T }{ 2 } \sum _{ i=1 }^{ N }{ { A }_{ i } }

Per cui:

h[n]=\sum _{ i=1 }^{ N }{ { T\cdot A }_{ i }\cdot { e }^{ n{ s }_{ i }T }u[n] } -\frac { T }{ 2 } \cdot h({ 0 }^{ + })\cdot \delta [n]=\\ =\sum _{ i=1 }^{ N }{ { T\cdot A }_{ i }\cdot { e }^{ n{ s }_{ i }T }u[n] } -\frac { T }{ 2 } \sum _{ i=1 }^{ N }{ { A }_{ i } }

Infine:

H(z)=\sum _{ i=1 }^{ N }{ \frac { { { T\cdot A } }_{ i } }{ 1-{ e }^{ { s }_{ i }T }{ z }^{ -1 } } } -\frac { T }{ 2 } \sum _{ i=1 }^{ N }{ { A }_{ i } }

dove:

\frac { T }{ 2 } \sum _{ i=1 }^{ N }{ { A }_{ i } }

è il termine correttivo che tiene conto del punti di discontinuità.

 

Fonti:

  • [Luise, M., & Vitetta, G. M. (2009). Teoria dei segnali (3ª ed.). McGraw-Hill Companies.]

 

⇐ Tecniche di progettazione IIR: Varianza Impulsiva

Tecniche di progettazione IIR: Trasformazione bilineare ⇒

Per questo articolo è tutto.

Per dubbi, errori o semplicemente ringraziamenti, puoi contattarci attraverso i nostri contatti social.

Puoi seguirci sul sito: www.antima.it
su Instagram: https://www.instagram.com/antima.it/
su Facebook: https://www.facebook.com/Antima.it/

Pubblicato

Scrivi un commento

Commento