In questo articolo si andrà a trattare la misura dell’impedenza caratteristica e determinazione della lunghezza di un cavo coassiale. Inoltre, si descriverà e realizzerà quello che viene definito come metodo riflettometrico.
Strumentazione
- Generatore di segnale Wavetek BDM40 (Serial Number: 900036);
- Oscilloscopio Tektronix TDS 210 (Serial Number: B122711);
- Reostato Samar CR/EDC2 (Serial Number: BL44);
- Matassa di cavo coassiale RG-58.
Circuito
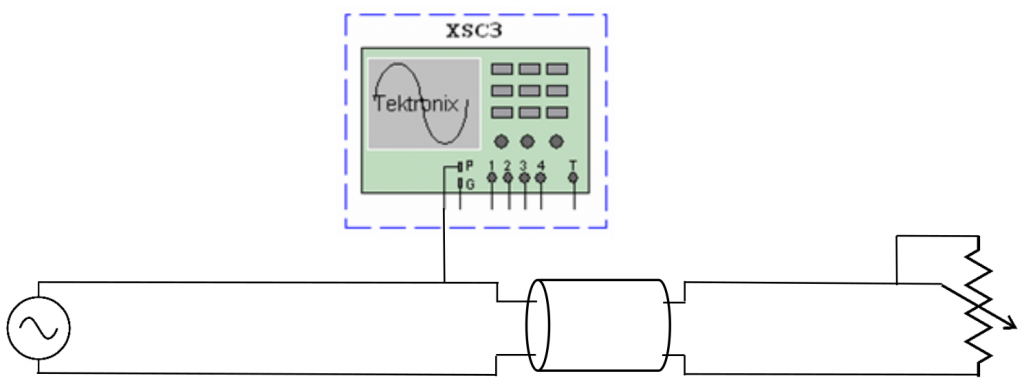
Considerazioni preliminari
Quando le dimensioni fisiche dei componenti di un circuito sono di molto inferiori rispetto alla lunghezza d’onda (alla frequenza di funzionamento), il circuito si dice a parametri concentrati; in questo caso le dimensioni fisiche dei componenti non influenzano il funzionamento del circuito.
Ciò non avviene quando le dimensioni fisiche dei componenti diventano comparabili con la lunghezza d’onda; in tal caso il circuito è detto a parametri distribuiti.
In questo caso è necessario ricorrere alle leggi dell’elettromagnetismo per studiare il comportamento del circuito.
Componente elettronico atto a trasportare segnali ed energia è la linea di trasmissione.
Se sono verificate opportune condizioni, è possibile trasmettere energia elettromagnetica lungo la suddetta linea (propagazione guidata).
Dalle leggi dell’elettromagnetismo è possibile ricavare e schematizzare un modello pratico di linea di trasmissione, che esprima la maggior parte dei fenomeni fisici.
Il modello è schematizzato come due conduttori paralleli che connettono un generatore V(x, t) ed un carico. In figura è mostrato un modello generale della linea di trasmissione:
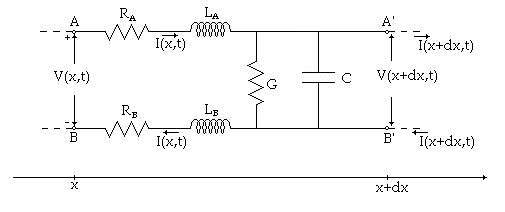
che presenta:
- Una resistenza per unità di lunghezza R [Ω/m]
- Un’induttanza per unità di lunghezza L [H/m]
Poiché si hanno due conduttori vicini, abbiamo un effetto capacitivo rappresentato da:
- Una capacità per unità di lunghezza C [F/m]
Poiché i conduttori sono separati da dielettrico, che presenta comunque imperfezioni, vi è una certa conducibilità tra i conduttori stessi, per cui:
- Una conduttanza per unità di lunghezza G [S/m]
R, L, C e G sono detti parametri distribuiti (o costanti primarie), poiché sono distribuiti lungo tutta la linea di trasmissione.
Considerando tratti infinitesimi di linea, R, L, C e G possono essere rappresentati dai corrispondenti elementi elettrici (parametri concentrati).
Il cavo coassiale RG58
Il cavo coassiale è una linea di trasmissione schermata, costituita da un conduttore cilindrico di rame a sezione circolare (anima) coassiale ad un conduttore esterno formato da una maglia metallica.
Il conduttore interno è separato da quello esterno da un dielettrico a bassa perdita (generalmente polietilene) che garantisce l’isolamento dei due conduttori.

In questa misura verrà utilizzato l’RG-58, un tipo di cavo coassiale utilizzato in larga misura per trasferire segnali elettrici con potenze fino a qualche centinaio di watt, in grado di lavorare in un range di frequenze relativamente ampio, spaziando dalla corrente continua fino a 2 GHz.
Il cavo ha una impedenza caratteristica di 50 o 60 Ω, con estremi dotati di connettori BNC.
Il reostato a decadi Samar
Il reostato è un resistore variabile; nella pratica si usa il termine reostato per indicare resistenze variabili tali da dissipare in calore una potenza elettrica non trascurabile.
Il Samar in questione è formato da un involucro con 5 manopole indicanti ognuna un ordine di grandezza: in particolare, si hanno decadi con 10 kΩ/step, 1 kΩ/step, 100 Ω/step, 10 Ω/step, 1 Ω/step.
Ogni singola manopola è costituita da una raggiera di resistori tutti con lo stesso valore R: con la sua rotazione è possibile muovere un contatto strisciante, selezionando così un numero diverso di resistenze, quindi un valore diverso di resistenza complessiva.
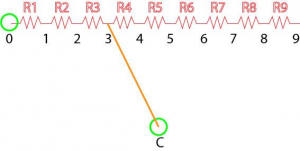
Le manopole risultano in serie tra di loro, permettendo così di realizzare un valore complessivo di resistenza andando a definirne tutti i valori, dall’unità alle decine di kΩ, e infine sommandoli.
Il fatto di poter scegliere la resistenza con un contatto strisciante offre un grande vantaggio, ovvero la possibilità di variare il valore di resistenza, in maniera più o meno continua, semplicemente spostando un cursore. Purtroppo lo svantaggio di un contatto strisciante del genere è la resistenza
residua più elevata, fattore che comporta un aumento dell’incertezza.
Per ogni manopola e, in particolare per ogni resistenza che la compone, sussisterà una determinata incertezza, indicata dal costruttore; l’incertezza complessiva sarà data dal contributo di ogni termine.
La misura
Si effettuano inizialmente i dovuti collegamenti: considerando che sulla linea andrà collegato sia il generatore di funzione che l’oscilloscopio, verrà utilizzato un particolare tipo di connettore a T, facilitando così la realizzazione dello schema e consentendoci di visualizzare l’onda viaggiante sulla linea di trasmissione.

L’altra estremità del cavo coassiale viene collegato al reostato tramite un adattatore BNC.
Completato il circuito, si procede con l’alimentazione, attendendo il dovuto tempo affinché tutti gli strumenti vadano a regime termico ed elettrico.
Sul generatore di funzioni viene impostato la forma d’onda quadra e con frequenze maggiori del MHz (lavorando sulle alte frequenze è lecito considerare l’impedenza caratteristica come puramente reale).
La scelta di usare la forma d’onda quadra è dovuta ad una questione di praticità e chiarezza di lettura.
Dalla teoria delle linee, in una linea adattata, ovvero una linea con impedenza caratteristica uguale all’impedenza di carico, il coefficiente di riflessione è nullo. Tale condizione fa sì che non ci sia onda riflessa sulla linea, ma soltanto onda diretta. Viceversa si ha nel caso di linea non adattata.
Nello schema realizzato, il reostato a decadi funge da impedenza di carico. Scopo dell’esperienza è quello di individuare il valore dell’impedenza caratteristica del cavo coassiale mediante adattamento della linea, ovvero mediante la determinazione dell’esatto valore di impedenza sul reostato.
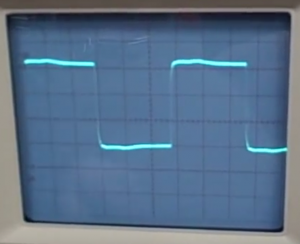
L’oscilloscopio servirà a valutare se il segnale, viaggiando lungo la linea, non venga riflesso e quindi sovrapposto all’onda diretta: modificando infatti tramite le manopole il valore di impedenza di carico, è possibile notare una variazione della forma d’onda.

L’espressione del coefficiente di riflessione in funzione dell’impedenza caratteristica della linea e quella di carico è:
grazie alla quale è possibile valutare matematicamente il comportamento dell’onda nei vari casi ricreati in laboratorio.
Per definizione Γ può assumere valori compresi tra -1 e 1:
Dall’oscilloscopio è possibile verificare inoltre che l’onda riflessa è in ritardo rispetto all’onda diretta, per come è stato realizzato il circuito.
Appurato che con un valore di 60 Ω si realizza l’adattamento della linea, si valuta l’incertezza di misura:
Per determinare la lunghezza del cavo coassiale, verrà applicato il metodo riflettometrico.
Si pone il circuito in condizione di linea aperta, dunque avremo nuovamente disadattamento e sull’oscilloscopio si misura ∆t=1μs, l’intervallo di tempo tra il fronte di salita dell’onda incidente e il fronte di salita dell’onda riflessa.
A questo punto si sostituisce il cavo coassiale con lunghezza incognita con un altro cavo di lunghezza nota (in questo caso di lunghezza L∗ = 9,9 m) e si misura ∆t∗ = 0,1 μs.
Da una semplice proporzione si ricava il valore della lunghezza incognita:
Ovviamente anche le misure effettuate su oscilloscopio sono affette da incertezza, la quale influenzerà il valore della lunghezza del cavo misurata indirettamente.
Ottenendo:
E infine: