Sintesi e dimensionamento PDN e PUN

Obiettivo di questo articolo è quello di chiarire il concetto di dimensionamento di una PDN (Pull-Down Network) e PUN (Pull-Up Network) illustrando un semplice approccio al problema.La tematica è molto specifica e fa parte degli argomenti di logica combinatoria e di sintesi dei circuiti digitali. In particolare, per avere un quadro generale dell’argomento, è possibile ideare un sistema digitale utilizzando due stili progettuali differenti:

• a logica statica: ovvero l’uscita del sistema è sempre connessa all’alimentazione (Vcc o GND). Ad esempio, Static CMOS, Pseudo-NMOS, Pass Transistor. In questo modo, esiste sempre un percorso diretto a bassa impedenza tra un potenziale dell’alimentazione e l’uscita. Ovviamente, il percorso verrà determinato in maniera complementare e non contemporaneamente, evitando la creazione di un cortocircuito dell’alimentazione.
• a logica dinamica: al contrario della logica statica, l’uscita non è sempre connessa all’alimentazione ma il dato viene temporaneamente memorizzato (immagazzinato) in una capacità sotto forma di carica.

Ci concentreremo sulla logica statica CMOS.

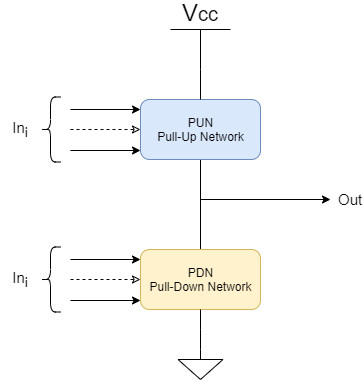
Esistono molte specifiche progettuali che una rete logica combinatoria dovrà rispettare, come ad esempio dissipazione di potenza statica idealmente nulla, robustezza ai disturbi e al rumore, tempi di salita e discesa etc.

Un altro punto riguarda il livello logico assunto dalla rete logica, quando dovrà assumere il livello alto e basso, 1 e 0 per intenderci. Infatti, è necessario far corrispondere al livello logico alto il potenziale alto dell’alimentazione, e al livello logico basso il riferimento a massa del circuito. Ciò si traduce in:

La PUN ha il compito di portare l’uscita a livello logico alto. La PDN ha il compito di portare l’uscita a livello logico basso. Considerando un generico ingresso, in funzione di esso si attiverà la PUN e disattiverà la PDN, portando l’uscita a livello alto oppure viceversa portando l’uscita verso il basso. Da notare che gli ingressi della PUN e PDN sono esattamente gli stessi, dunque per lo stesso ingresso le due reti funzioneranno in maniera logicamente opposta.

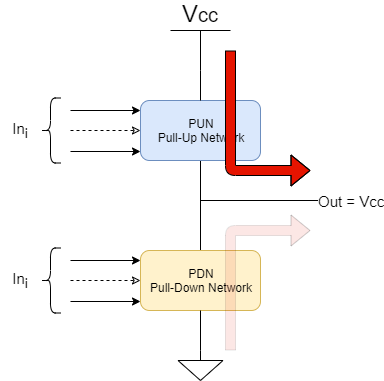
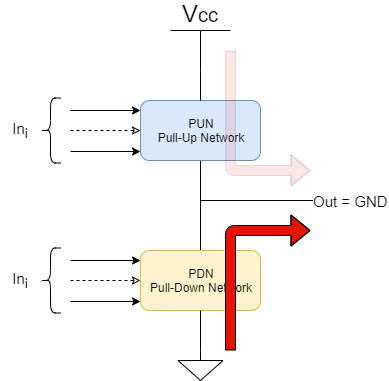
Le due reti permettono quindi di ottenere l’uscita come funzione logica degli ingressi utilizzando la logica CMOS. Si possono creare porte logiche semplici o più complesse, realizzando le reti con quella specifica logica.

Il singolo transistor CMOS può essere infatti visto come un semplice switch controllato dal segnale sul gate. La combinazione di questi CMOS in serie o parallelo implementa le semplici funzioni logiche come una AND o una OR, come illustrato in seguito.

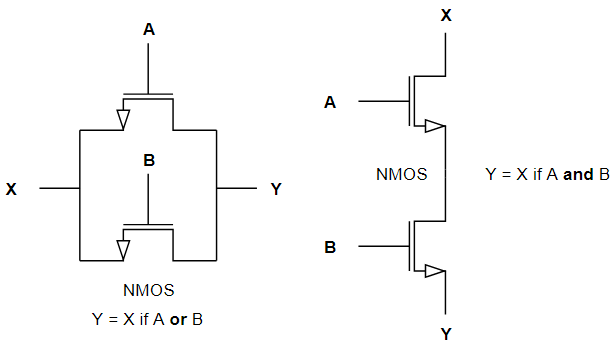
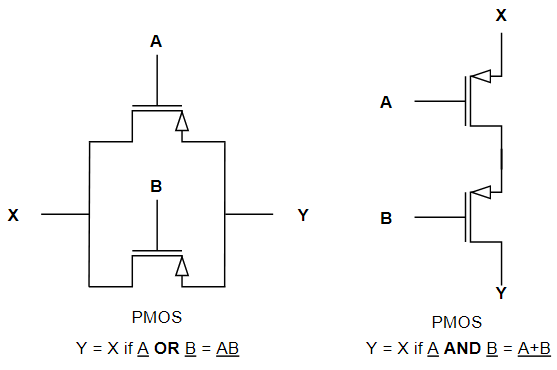
Come visibile, è possibile utilizzare una logica a NMOS o a PMOS per implementare una qualsiasi funzione logica. Dalle caratteristiche fisiche ed elettriche intrinseche negli NMOS e PMOS però c’è una sostanziale differenza: gli NMOS passano uno 0 forte ma un 1 debole, mentre i PMOS passano un 1 forte ma uno 0 debole.

Ciò potrebbe andare in contrasto con le specifiche tecniche precedentemente affermate, in particolare quella per cui Voh=Vcc e Vlh=0. Per questo motivo vengono utilizzate le reti PUN e PDN, permettendo in ogni caso e condizione di avere un uscita perfettamente in linea con il livello logico atteso.

Risulta ovvio e motivato quindi l’utilizzo di NMOS per la realizzazione di PDN e l’utilizzo di PMOS per le PUN. Per gli esempi fatti precedentemente, una NAND sarebbe così formata:

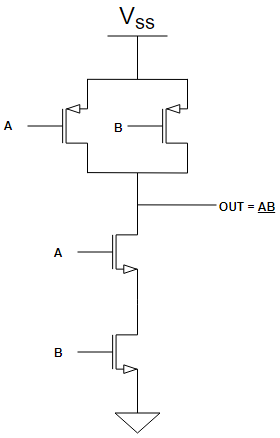
Un tipico approccio nella sintesi di questi circuiti fa l’uso del modello a switch, sostituendo i transistor con degli switch in serie ad una resistenza. Ciò è valido supponendo che il transistor in conduzione si trovi in regione lineare. In questo modo si simula il comportamento dei transistor mantenendo l’aspetto resistivo. La presenza della resistenza (e di altri elementi come capacità parassite non considerate nello schema) permette di aggiungere una nuova considerazione, ovvero quella dei ritardi o delay.

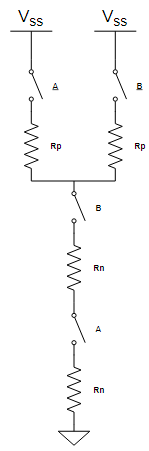
Il passaggio del segnale attraverso un transistor (e quindi nel modello a switch una resistenza) comporta un certo ritardo (tempo di propagazione). Maggiore è il valore di queste resistenze, maggiore sarà il delay. Da notare che si hanno casi in cui i transistor risultano in serie per cui il ritardo complessivo sarà maggiore.

È possibile prevedere e agire sul valore di queste resistenze andando ad analizzare le caratteristiche geometriche dei transistor, ovvero sulla larghezza W e lunghezza L del canale.

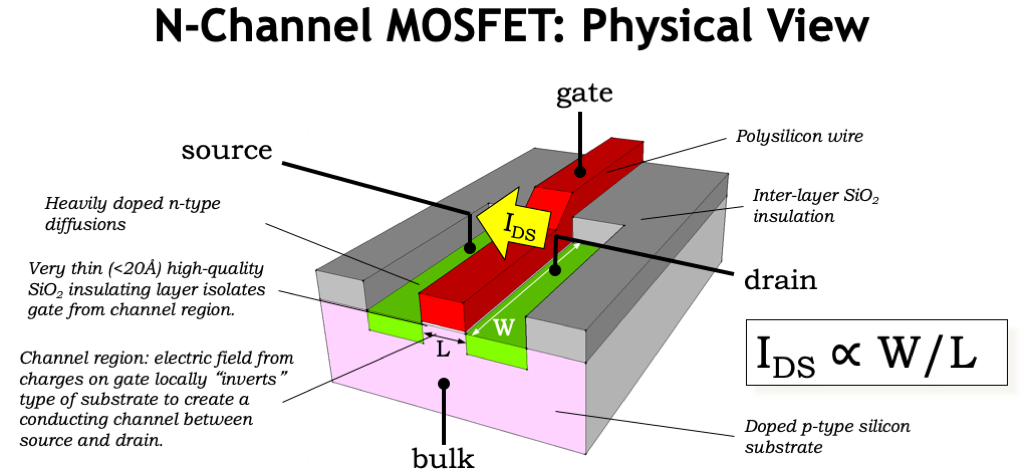
Come visibile in figura la corrente in grado di scorrere attraverso il transistor è proporzionale al rapporto delle caratteristiche geometriche W/L. La relativa resistenza è funzione della corrente e quindi di questo rapporto W/L. Siccome la larghezza e la lunghezza del canale sono parametri che è possibile scegliere quasi arbitrariamente in fase di realizzazione di un CMOS, ci si avvale di essi per minimizzare quanto più possibile i tempi di propagazione.

Fatte queste dovute premesse, possiamo focalizzare la nostra attenzione sulla progettazione di un circuito basato su PDN e PUN con relativo dimensionamento andando a formalizzare, passo dopo passo, cosa fare.

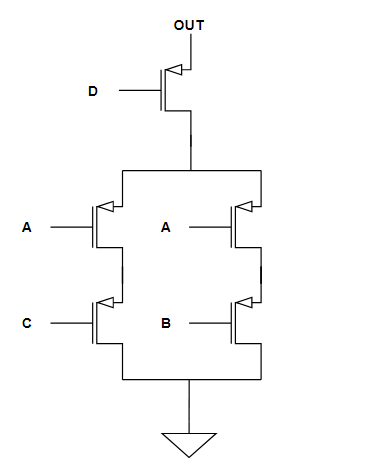
Sia data una funzione logica da implementare, ad esempio F = (AB+AC)+D. Si realizzi la PDN e PUN dimensionandone i CMOS.

Realizzare PDN e PUN

Si parte dall’operazione più interna, andando ad includere via via quelle più esterne. Possiamo partire arbitrariamente dalla PDN o dalla PUN, saranno complementari.

Consideriamo prima la PDN. Sapendo che la PDN è formata da NMOS, avremo che:

• AB = serie di NMOS;
• AC = serie di NMOS;
• AB + AC = parallelo dei NMOS;
• (AB + AC) + D = serie dei NMOS.

Otteniamo così:

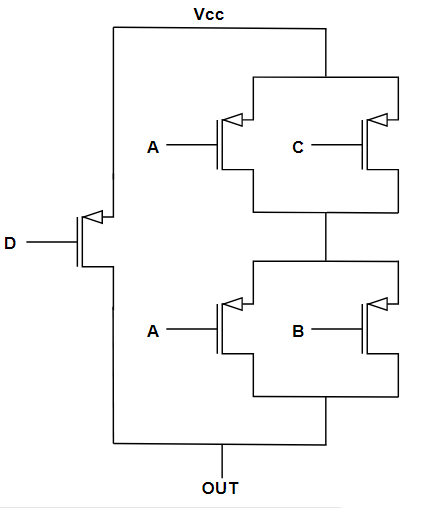
Consideriamo ora la PUN. Sapendo che la PUN è formata da PMOS, avremo che:

• AB = parallelo di PMOS;
• AC = parallelo di PMOS;
• AB + AC = serie dei PMOS;
• (AB + AC) + D = parallelo dei PMOS.

Otteniamo così:

In questo modo abbiamo realizzato le due reti di Pull-Down e Pull-Up.

Dimensionamento delle reti

La rete di Pull-Up dovrà essere necessariamente più grande della rete di Pull-Down, rispettando la condizione di dimensionamento minimo (ovvero assegnare il più piccolo valore possibile ai singoli CMOS).

Si può partire a dimensionare arbitrariamente la PDN o la PUN, è indifferente. Se si parte dalla PDN, si considera la PUN il doppio, altrimenti se si parte dalla PUN, si considera la PDN la metà.

Consiglio di partire dalla PDN e considerare l’intera rete con dimensione 1. I valori che verranno assegnati sono numeri interi positivi ottenuti normalizzando la dimensione del canale a 1.

Suddivisione delle reti

All’interno della singola rete, si può suddividere idealmente il circuito in sottoreti in questo modo:

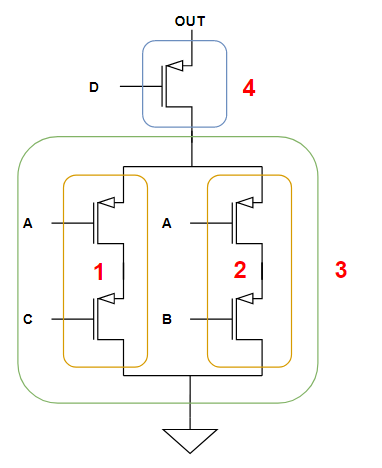
dove:

• 1 e 2 sono le sottoreti più interne;
• 3 il parallelo;
• 4 il transistor isolato in serie.

Regole per il dimensionamento

Nel dimensionare, bisogna rispettare alcune regole:

• la serie di transistor viene dimensionata come un parallelo. Esempio, nella sottorete 1, se si dimensionano i due transistor con valore 2 e 2, complessivamente la sottorete avrà valore 1!
• i rami in parallelo devono avere uguale dimensione. Esempio, considerando la sottorete 1, con dimensione 1, allora anche la sottorete 2 sarà complessivamente di dimensione 1, e quindi i transistor che la compongono avranno dimensione 2.
• una sottorete formata da paralleli ha la stessa dimensione di uno dei rami in parallelo che la forma (sono uguali).

Si può dimensionare sia con valori pari che dispari, con i pari risulta però più semplice.

Applicazione delle regole

Ritornando all’esempio, applichiamo le regole viste:

1. Partiamo dalla rete complessiva, ricordando che deve valere 1;
2. Successivamente individuiamo le sottoreti 4 e 3, che sono in serie tra loro.
3. Dalla prima regola, possiamo dedurre che se la PDN deve valere 1 come dimensione, allora le sottoreti 4 e 3 devono valere necessariamente 2, in quanto 2 // 2 = 1. La sottorete 4 è completamente dimensionata.
4. Consideriamo la sottorete 3, che ha dimensione 2. Iteriamo le considerazioni fatte precedentemente a questa sottorete.
5. Individuiamo le sottoreti 1 e 2, che sono in parallelo tra loro.
6. Per la regola 2, basterà dimensionare una delle due sottoreti, l’altra sarà uguale. Consideriamo la sottorete 1 che è formata dalla serie di A e B.
7. Dalla terza regola, le sottoreti 1 e 2 devono avere la stessa dimensione della sottorete 3, ovvero pari a 2. Dunque A e B, che sono in serie, devono rispettare il fatto che la loro sottorete deve avere dimensione pari a 2.
8. Dalla prima regola, per avere dimensione 2, il loro “parallelo” deve valere 4 in quanto 4 // 4 = 2. Nello stesso modo, la sottorete formata da A e C.

Alla fine, otterremo la PDN totalmente dimensionata come segue:

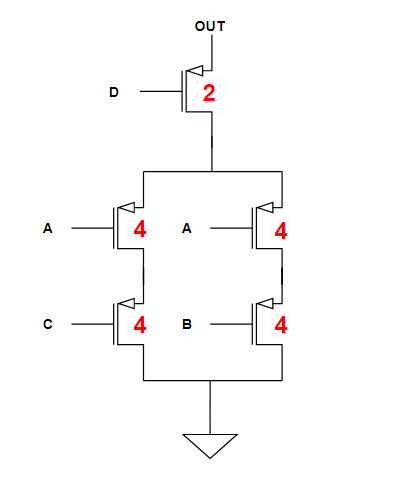
Per questo articolo è tutto.

Per dubbi, errori o semplicemente ringraziamenti, puoi contattarci attraverso i nostri contatti social.