in Elettronica |

Tecniche di progettazione FIR

In questo articolo si andranno a introdurre concetti base per la progettazione di filtri digitali di tipo FIR.

Nei precedenti articoli abbiamo trattato i filtri digitali IIR (Infinite Impulse Response) con alcuni approcci teorici e progettuali. Si andrà ora a descrivere invece la tipologia FIR (Finite Impulse Response).

In genere, si utilizzano filtri IIR se è richiesta una certa risposta in ampiezza, piuttosto che in fase. Se le specifiche di progetto richiedono invece una determinata risposta in frequenza e/o una certa linearità in fase, si utilizzano filtri FIR.

Si suppone di voler realizzare un filtro passa-basso. La risposta impulsiva e in frequenza sarà:

{ h }_{ ID }[n]=2BTsinc(2nBT)\quad \Leftrightarrow \quad \overline { { H }_{ ID } } (f)=\sum _{ k }^{ \quad }{ rect\left( \frac { f-\frac { k }{ T } }{ 2B } \right) }

ovvero un filtro IIR, non causale e quindi non realizzabile.

È possibile ottenere una approssimazione del filtro ideale trascurando (considerandoli nulli) i valori di hID[n] per |n|>L con L arbitrario, ottenendo hS[n]. In tal modo, si ottiene un filtro FIR non causale, con risposta impulsiva simmetrica ottenuta da hID[n] per troncamento. 

{ h }_{ s }[n]=\begin{cases} { h }_{ ID }[n]=2BTsinc(2nBT)\qquad \left| n \right| \le L \\ 0\qquad \qquad \qquad \qquad \qquad \quad \quad altrimenti \end{cases}

Ciò comporta una differente risposta in frequenza.

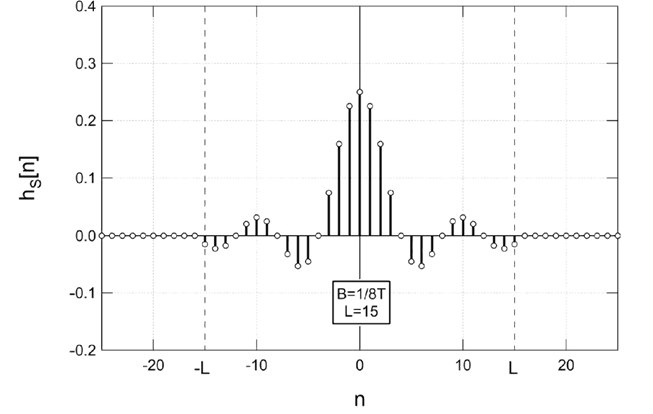
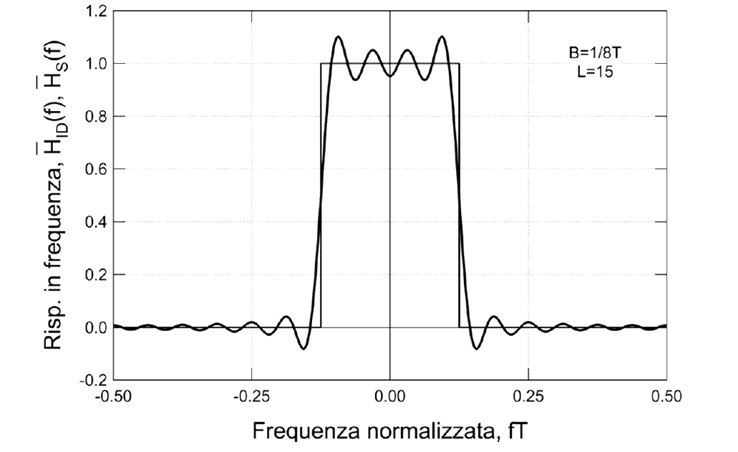
Risposta impulsiva ottenuta per troncamento
Differenza tra la risposta in frequenza ideale e quella ottenuta per troncamento di un filtro passa-basso

Per rendere h[n] ottenuto anche causale, si effettua una traslazione (shift) verso destra di L campioni.

h[n]={ h }_{ s }[n-L]=\begin{cases} 2BTsinc(2(n-L)BT)\qquad 0\le n\le L \\ 0\qquad \qquad \qquad \qquad \qquad \quad \quad altrimenti \end{cases}

Fonti:

  • [Luise, M., & Vitetta, G. M. (2009). Teoria dei segnali (3ª ed.). McGraw-Hill Companies.]

 

⇐ Tecniche di progettazione IIR: Trasformazione bilineare

Per questo articolo è tutto.

Per dubbi, errori o semplicemente ringraziamenti, puoi contattarci attraverso i nostri contatti social.

Puoi seguirci sul sito: www.antima.it
su Instagram: https://www.instagram.com/antima.it/
su Facebook: https://www.facebook.com/Antima.it/

Pubblicato

Scrivi un commento

Commento

    • Ciao Francesco, presto tratterò l’implementazione di queste tecniche tramite Matlab. Ci sto lavorando su. Continua a seguirci per rimanere aggiornato!

      Rispondi a Andrea