in Elettronica |

Tecniche di progettazione IIR: Invarianza Impulsiva

In questo articolo si andrà a illustrare una prima tecnica di progettazione per filtri digitali IIR, ovvero il metodo della invarianza impulsiva.

Come introdotto nel precedente articolo, esistono diverse tipologie di filtri digitali e diverse tecniche di progettazione per ciascuno di essi. 

Dato un sistema a tempo continuo e la sua risposta impulsiva ha(t) si ottiene la risposta impulsiva h[n] del sistema a tempo discreto campionando la risposta a tempo continuo ha(t) con un opportuno periodo T.

h[n]=T\cdot { h }_{ a }(nT)\quad \Rightarrow \quad \overline { H } (f)=\sum _{ -\infty }^{ \infty }{ { H }_{ a }\left( f-\frac { k }{ T } \right) }

Si portano in evidenza alcuni aspetti legati ai termini utilizzati. La risposta impulsiva a tempo continuo è stata indicata con ha(t), esprimendone il suo legame temporale. Il pedice a indica che si tratta di una risposta ottenuta con tecniche analogiche. La risposta impulsiva a tempo discreto è stata indicata con h[n], esprimendo il legame con i campioni n, racchiusi utilizzando parentesi quadre.

Se ha(t) è limitata in banda e il periodo di campionamento rispetta la condizione di Nyquist, allora il filtro a tempo discreto ha le stesse caratteristiche di selettività del filtro analogico, poiché non insorge l’aliasing.

Per la fisica realizzabilità, i prototipi analogici sono filtri causali e la loro risposta in frequenza non può essere limitata in banda.

Aliasing [1]

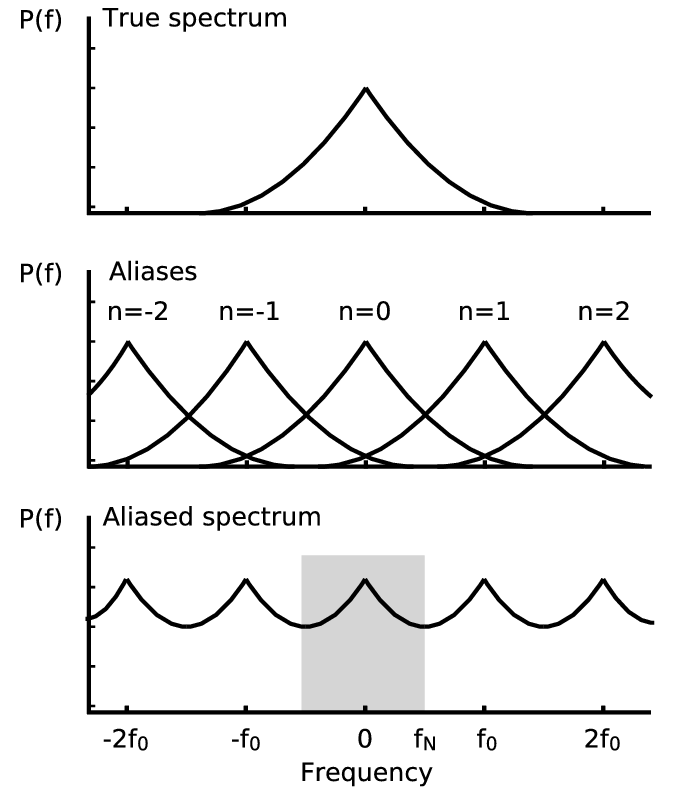
La tecnica della invarianza impulsiva è dunque applicabile a filtri con limite superiore di banda, quindi impraticabile per filtri passa-alto o elimina-banda.

Si può ricavare direttamente la funzione di trasferimento H(z) del filtro a tempo discreto se il prototipo analogico ha una funzione di trasferimento Ha(s) razionale fratta in s, senza calcolare ha(t). Consideriamo in generale:

{ H }_{ a }(s)=\frac { N(s) }{ D(s) } =\frac { { \beta }_{ 0 }+{ \beta }_{ 1 }\cdot s+…+{ \beta }_{ M }\cdot { s }^{ M } }{ { \alpha }_{ 0 }+{ \alpha }_{ 1 }\cdot s+…+{ \alpha }_{ N }\cdot { s }^{ N } } =\sum _{ i=1 }^{ N }{ \frac { { A }_{ i } }{ s-{ s }_{ i } } }

dove:

  • Ai =residuo del polo;
  • si =poli tempo continuo;
  • esiT=poli a tempo discreto.

Antitrasformando:

 

{ h }_{ a }(t)=\sum _{ i=1 }^{ N }{ { A }_{ i }{ e }^{ { s }_{ i }T }u(t) }

Campionando:

{ h }[n]=\sum _{ i=1 }^{ N }{ T{ A }_{ i }{ e }^{ n{ s }_{ i }T }u[n] }

Applicando la trasformata zeta:

{ H }(z)=\sum _{ i=1 }^{ N }{ \frac { T{ A }_{ i } }{ 1-{ e }^{ { s }_{ i }T }{ z }^{ -1 } } }

Applichiamo il procedimento per ottenere un filtro passa-basso discreto:

Filtro passa-basso RC analogico

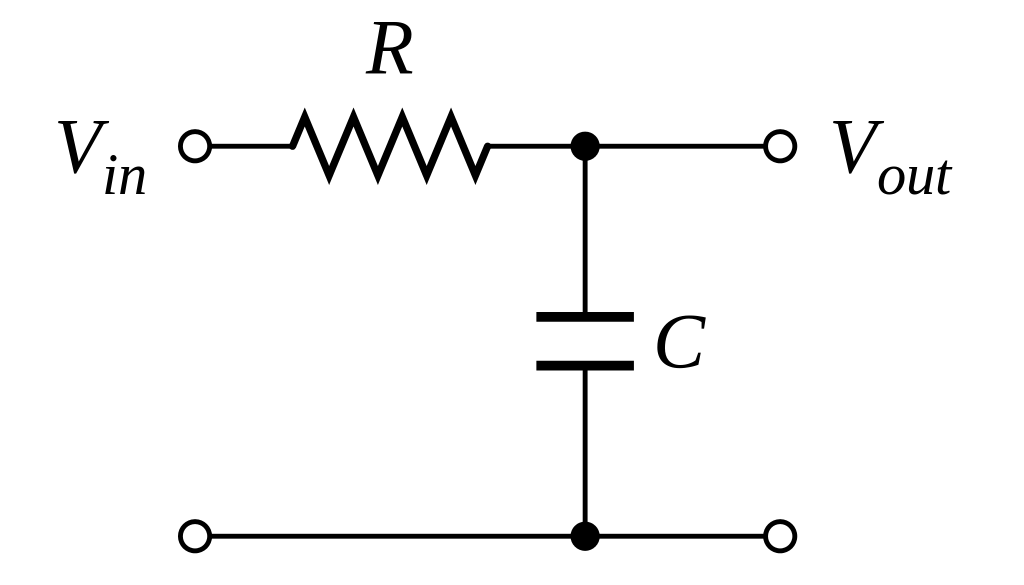
Sappiamo che nel dominio di Laplace vale:

{ { H }_{ a } }(s)=\frac { 1 }{ \alpha s+1 } =\frac { \frac { 1 }{ \alpha } }{ s+\frac { 1 }{ \alpha } }

dove α=RC. Applicando l’invarianza impulsiva si ha:

{ H }(z)=\sum _{ i=1 }^{ N }{ \frac { T{ A }_{ i } }{ 1-{ e }^{ { s }_{ i }T }{ z }^{ -1 } } }

con:

\begin{cases} { A }_{ i }=1 \\ { s }_{ i }=-\frac { 1 }{ \alpha } \\ N=1 \end{cases}

Per cui otteniamo:

{ H }(z)=\frac { T }{ \alpha } \frac { 1 }{ 1-{ e }^{ -\frac { T }{ \alpha } }{ z }^{ -1 } }

Siccome il prototipo analogico non ha banda rigorosamente limitata, per ridurre l’aliasing è necessario scegliere opportunamente la frequenza di campionamento nei confronti della banda del filtro a 3db:

{ B }_{ 3db }=\frac { 1 }{ 2\pi \alpha }

Per questa tipologia di filtri è consiglibile usare un valore di fc maggiore di un valore di 5∼10 rispetto a quello di Nyquist.

Fonti:

  • [1] Spatial aliasing and distortion of energy distribution in the wave vector domain under multi-spacecraft measurements – Scientific Figure on ResearchGate.
    Available from: https://www.researchgate.net/figure/Illustration-of-aliasing-in-the-frequency-domain-A-true-spectrum-top-panel-appears_fig1_41137052 [accessed 28 Feb, 2020].

 

  • [Luise, M., & Vitetta, G. M. (2009). Teoria dei segnali (3ª ed.). McGraw-Hill Companies.]

⇐ Filtri FIR e IIR – Una breve introduzione

Tecniche di progettazione IIR: Varianza Impulsiva – Ulteriori considerazioni  ⇒

Per questo articolo è tutto.

Per dubbi, errori o semplicemente ringraziamenti, puoi contattarci attraverso i nostri contatti social.

Puoi seguirci sul sito: www.antima.it
su Instagram: https://www.instagram.com/antima.it/
su Facebook: https://www.facebook.com/Antima.it/

Pubblicato

Scrivi un commento

Commento