In questo articolo verrà esposto un metodo di misura della costante di tempo in un circuito RC al variare della frequenza.
L’obiettivo è verificare e analizzare gli effetti parassiti in un circuito RC e la loro relativa influenza nel calcolo della costante di tempo τ al variare della frequenza.
Inoltre, verrà determinato il valore della frequenza oltre la quale tali effetti alterano significativamente la costante di tempo τ.
Strumentazione
- Generatore di segnale TEKTRONIX CFG253 3MHz (Serial Number CFG-253 TW60112);
- Oscilloscopio TEKTRONIX TDS210 60MHz 1GHz/s (Serial Number C041238);
- Cavi di collegamento con connettore a banana;
- Sonda con connettore BNC.
Componenti utilizzati
- Resistenza R;
- Condensatore C (4,7μF).
Schema circuitale
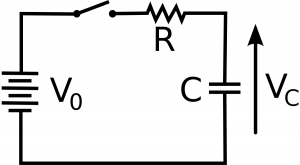
La misura
Obiettivo di questa esperienza è quello di dimostrare che i valori delle impedenze dipendono dalla frequenza di lavoro.
Infatti, nonostante si possano approssimare con valori costanti di capacità e resistenza per piccole variazioni di frequenza, per variazioni significative di frequenza tale approssimazione non sarà più valida.
È possibile verificare che soltanto fino ad una determinata frequenza la costante di tempo τ assume un valore pressoché costante.
Si procede inizialmente alla realizzazione del circuito, collegando il generatore di funzioni, tramite i cavi, all’impedenza RC serie.
All’uscita del generatore di funzioni (boccola MAIN) si collega l’adattatore BNC rosso/nero. Alla boccola nera dell’adattatore si collega il terminale negativo del condensatore C, alla boccola rossa invece l’estremità della resistenza R.
La misura prevede l’utilizzo dell’oscilloscopio: tramite apposita sonda BNC si collega l’estremità nera alla massa del circuito e l’uncino (parte calda) all’altra estremità dell’impedenza. Ultimati i collegamenti, si accendono gli strumenti e si attende affinché il circuito vada a regime termico ed elettrico.
Si setta la frequenza del generatore di funzioni ad un valore f = 50Hz, fissando il valore di fondo scala a 100 Hz e regolando la manopola a 0,5, e ad una tensione arbitraria che in questa sede sarà di 10 Volt picco-picco (Vmax = 5 Volt).
Si aumenta la frequenza del generatore fino alla massima frequenza generabile dallo strumento e il passo lo si stabilisce nel seguente modo: se la tensione Vc max, all’aumentare della frequenza, varia in modo significativo, si deve accorciare il passo di variazione; se invece la tensione Vc max non varia in modo significativo, si può aumentare il passo.
Si misura la tensione erogata, che in questa configurazione circuitale sarà pari alla caduta di tensione su tutto il ramo RC. Successivamente si effettua la misurazione della caduta di tensione ai capi del condensatore, utilizzando sempre la sonda dell’oscilloscopio.
Si riporta in tabella i dati relativi alle misurazioni:
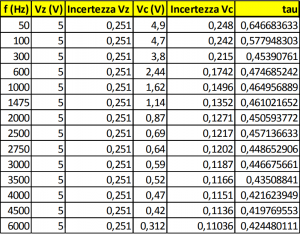
Per il calcolo delle incertezze Vz e Vc, si sono seguite le specifiche relative all’oscilloscopio TEKTRONIX TDS210 60MHz 1GHz/s, con il quale si è effettuata la misura.
In particolare si sono definiti i valori di incertezza Vz e Vc basandosi sulla seguente tabella:
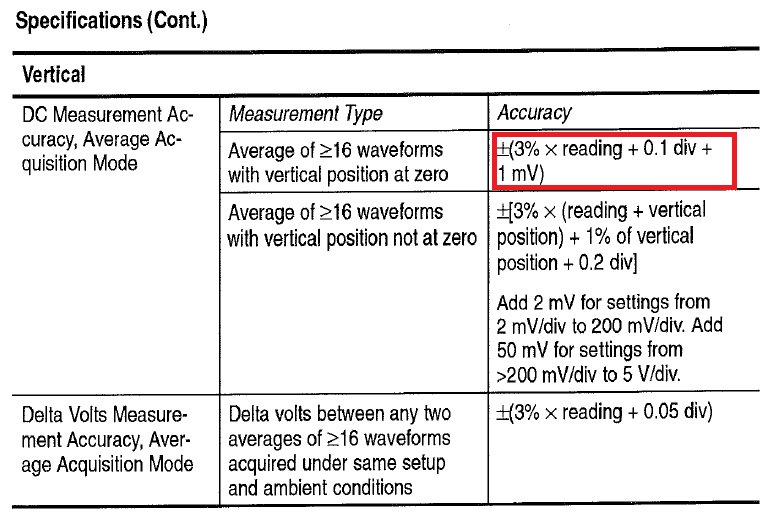
La misura diretta di una certa grandezza presuppone la progettazione di un’esperienza con la quale eseguire direttamente misure su di essa. Ciò spesso non è realizzabile. Si rende allora necessario un metodo di misura indiretto basato sul fatto che la grandezza da studiare è legata ad altre quantità, che sono misurabili direttamente, tramite una equazione matematica.
Dunque, per valutare la costante di tempo τ, ci si serve dei valori massimi di tensione ai capi della resistenza e dell’impedenza, sfruttando le seguenti considerazioni analitiche:
\frac { \dot { { V }_{ C } } }{ \dot { { V }_{ Z } } } =\frac { \frac { j }{ \omega C } }{ R-\frac { j }{ \omega C } } =\frac { -j }{ \omega RC-j } =\frac { 1 }{ 1+j\omega RC }
Valutandone il modulo:
\left| \frac { \dot { { V }_{ C } } }{ \dot { { V }_{ Z } } } \right| =\frac { { V }_{ Cmax } }{ { V }_{ Zmax } } =\sqrt { \frac { 1 }{ 1+{ \omega }^{ 2 }{ R }^{ 2 }C^{ 2 } } } =\sqrt { \frac { 1 }{ 1+{ \omega }^{ 2 }{ \tau }^{ 2 } } }
Da cui:
1+{ \omega }^{ 2 }{ \tau }^{ 2 }={ \left( \frac { { V }_{ Zmax } }{ { V }_{ Cmax } } \right) }^{ 2 }
Infine:
\tau =\frac { 1 }{ \omega } \sqrt { { \left( \frac { { V }_{ Zmax } }{ { V }_{ Cmax } } \right) }^{ 2 }-1 }
Per ogni valore di frequenza, si è calcolato il relativo valore della costante di tempo τ. Con tutti questi dati in possesso, si è infine calcolata l’incertezza sui valori ricavati di τ, con la seguente formula:
U(\tau )=\sqrt { { \left( \frac { \partial \tau }{ { \partial V }_{ Zmax } } \right) }^{ 2 }{ (U({ V }_{ Zmax })) }^{ 2 }+{ \left( \frac { \partial \tau }{ { \partial V }_{ Cmax } } \right) }^{ 2 }{ (U({ V }_{ Cmax })) }^{ 2 }+{ \left( \frac { \partial \tau }{ \partial f } \right) }^{ 2 }{ (U(f)) }^{ 2 } }
Per semplicità, vengono calcolati separatamente i contributi di ogni termine:
\bullet \quad \frac { \partial \tau }{ { \partial V }_{ Zmax } } =\frac { \partial }{ { \partial V }_{ Zmax } } \left[ \frac { 1 }{ \omega } \sqrt { { \left( \frac { { V }_{ Zmax } }{ { V }_{ Cmax } } \right) }^{ 2 }-1 } \right] =\frac { 1 }{ \omega } \frac { { V }_{ Zmax } }{ { { V }_{ Cmax } }^{ 2 }\sqrt { { \left( \frac { { V }_{ Zmax } }{ { V }_{ Cmax } } \right) }^{ 2 }-1 } } \bullet \quad U({ V }_{ Zmax })=\pm \left( 3\%reading+0,1div+1mV \right) \bullet \quad \frac { \partial \tau }{ { \partial V }_{ Cmax } } =\frac { \partial }{ { \partial V }_{ Cmax } } \left[ \frac { 1 }{ \omega } \sqrt { { \left( \frac { { V }_{ Zmax } }{ { V }_{ Cmax } } \right) }^{ 2 }-1 } \right] =-\frac { 1 }{ \omega } \frac { { V }_{ Zmax } }{ { { V }_{ Cmax } }^{ 2 }\sqrt { { \left( \frac { { V }_{ Zmax } }{ { V }_{ Cmax } } \right) }^{ 2 }-1 } } \bullet \quad U({ V }_{ Cmax })=\pm \left( 3\%reading+0,1div+1mV \right) \bullet \quad \frac { \partial \tau }{ \partial f } =\frac { \partial }{ \partial f } \left[ \frac { 1 }{ \omega } \sqrt { { \left( \frac { { V }_{ Zmax } }{ { V }_{ Cmax } } \right) }^{ 2 }-1 } \right] =-\frac { \sqrt { { \left( \frac { { V }_{ Zmax } }{ { V }_{ Cmax } } \right) }^{ 2 }-1 } }{ 2\pi { f }^{ 2 } } \bullet \quad U(f)=\pm 5\%\quad of\quad full\quad scale\quad of\quad frequency
Dalla variazione del valore di τ, si è tracciato un grafico in funzione della frequenza:
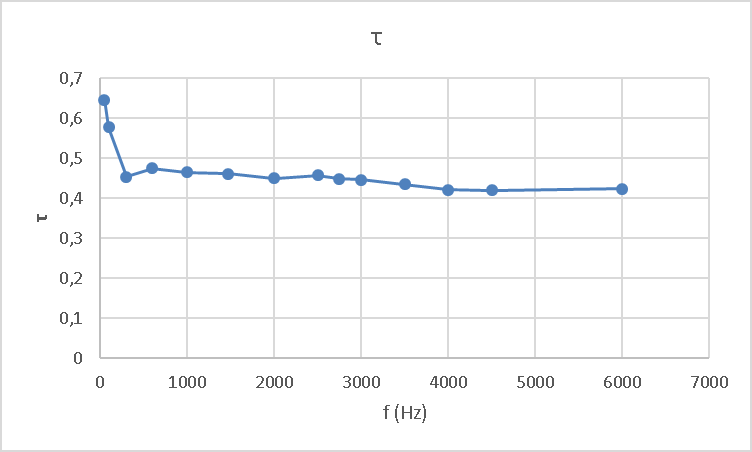
Concludendo, è possibile notare come la costante di tempo τ rimanga costante ma, per determinate frequenze, subisca alcuni effetti parassiti che dipendono appunto dalla frequenza a cui si lavora.