Tutorial – Misura di impedenza con il metodo industriale

In questo articolo verrà esposto un metodo di misura, analisi e determinazione di un’impedenza secondo il metodo industriale.

Strumentazione

• Oscilloscopio TEKTRONIX TDS210 60MHz 1GHz/s (Serial Number C041238);
• Multimetro Wavetek BDM40 (Serial Number: 01100105);
  Trasformatore;
• Cavi di collegamento con connettore a banana;
• Sonda con connettore BNC.

 

Componenti utilizzati

• 2 x Resistenze R e Rx;
• Condensatore Cx (4,7μF).

 

Circuito

 

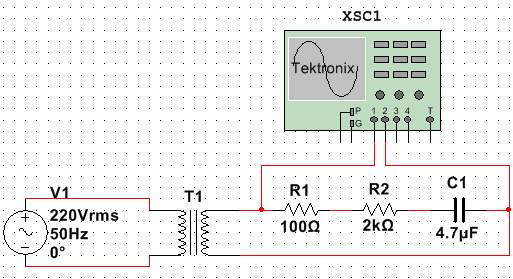
La misura

Si procede inizialmente alla realizzazione del circuito, collegando il trasformatore alla presa da 220 V (50 Hz).
Il trasformatore è dotato di tre uscite disposte in fila: la centrale è la massa comune, mentre ai lati si ha la possibilità di avere 10V oppure 12V.
Nel corso di questa misura si è scelto arbitrariamente l’uso dell’uscita da 10 V.
Tra i 10V e la massa del trasformatore, si è realizzato un circuito serie composto dalle 2 resistenze e dal condensatore, tenendo conto della sua polarità.
Si considera la serie Rx-Cx come una impedenza di tipo ohmico-capacitivo Zx, di cui dovremo ricavare il valore tramite il metodo industriale, supponendo di non conoscerne la natura e i valori.

Completato il circuito, si procede con l’alimentazione, attendendo il dovuto tempo affinché tutti gli strumenti vadano a regime termico ed elettrico.
Si procede con la misura del valore della resistenza RC e Rx tramite multimetro, valutandone le relative incertezze, considerando le direttive del datasheet del multimetro:

\bullet \quad { R }_{ C }=101,77\Omega \\ \bullet \quad U({ R }_{ C })=0,1\%\quad of\quad reading+4\quad digit=0,10177+0,04=0,14\\ \bullet \quad { \sigma }_{ X }=\pm \frac { U({ R }_{ C }) }{ \sqrt { 3 } } =\pm 0,08

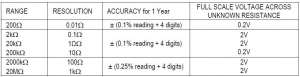
Quindi avremo:

{ R }_{ C }=(101,77\pm 0,08)\Omega

Viene inoltre misurato il valore della tensione in uscita dal trasformatore, pari a 9,75 V.

Completato il circuito, vengono effettuate le misure: l’oscilloscopio in dotazione è dotato di due canali, con i quali è possibile vedere e confrontare contemporaneamente due segnali diversi.
Viene prelevata con la prima sonda la caduta di tensione sull’impedenza e con la seconda quella sulla resistenza campione, mandando i segnali rispettivamente sul primo e il secondo canale.
È necessario collegare le masse di entrambe le sonde sul morsetto comune all’impedenza da misurare e alla resistenza campione per evitare un cortocircuito della resistenza.

Ultimati i preparativi si procede con la lettura dei dati dal display dell’oscilloscopio con la relativa incertezza di misura, calcolata secondo le indicazioni della seguente tabella.

\bullet \quad { \sigma }_{ { V }_{ Zmax } }=\pm \frac { U({ V }_{ Zmax }) }{ \sqrt { 3 } } =\pm \frac { 3\%\quad of\quad reading+0,1div+1mV }{ \sqrt { 3 } } =\pm 0,235\\ \\ \bullet { \quad V }_{ Zmax }=(13,5\pm 0,235)V\\ \\ \bullet \quad { \sigma }_{ { V }_{ RCmax } }=\pm \frac { U({ V }_{ RCmax }) }{ \sqrt { 3 } } =\pm \frac { 3\%\quad of\quad reading+0,1div+1mV }{ \sqrt { 3 } } =\pm 0,012\\ \\ \bullet { \quad V }_{ RCmax }=(0,62\pm 0,012)V

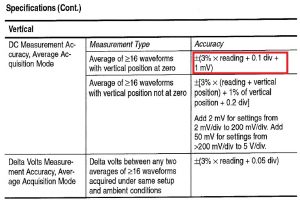
Una generica impedenza è definita come:

{ Z }_{ X }={ R }_{ X }\pm { jX }_{ X }

dove:

{ R }_{ X }=parte\quad reale\quad dell’impedenza\quad (tipo\quad ohmico)\\ { X }_{ X }=parte\quad immaginaria\quad dell’impedenza\quad (reattanza\quad induttiva\quad o\quad capacitiva)\\ j=unità\quad immaginaria

La scelta del segno dipende dalla natura della reattanza: segno positivo per reattanza induttiva e segno negativo per reattanza capacitiva.
Risolvendo il circuito si ha:

\dot { V } =\dot { { V }_{ { R }_{ C } } } +\dot { { V }_{ { Z }_{ X } } } =({ R }_{ C }+\dot { { Z }_{ X } } )\dot { I }

Supponendo la condizione

{ R }_{ C }\ll \left| { Z }_{ X } \right|

Si potrà semplificare l’espressione precedente:

\dot { { V }_{ { Z }_{ X } } } =\dot { { Z }_{ X } } \cdot \dot { I }

da cui:

\dot { { Z }_{ X } } =\frac { \dot { V } }{ \dot { I } }

Valutando il modulo dell’impedenza, si avrà:

\left| { Z }_{ X } \right| =\frac { { V }_{ Zmax } }{ { V }_{ Rmax } } \cdot { R }_{ C }

Si calcola inoltre la relativa incertezza indiretta:

U(\left| { Z }_{ X } \right| )=\sqrt { { \left( \frac { \partial \left| { Z }_{ X } \right| }{ \partial { V }_{ Zmax } } \right) }^{ 2 }{ \left( U({ V }_{ Zmax }) \right) }^{ 2 }+{ \left( \frac { \partial \left| { Z }_{ X } \right| }{ \partial { V }_{ Rmax } } \right) }^{ 2 }{ \left( U({ V }_{ Rmax }) \right) }^{ 2 }+{ \left( \frac { \partial \left| { Z }_{ X } \right| }{ \partial { R }_{ C } } \right) }^{ 2 }{ \left( U({ R }_{ C }) \right) }^{ 2 } }

Per semplicità, vengono calcolati separatamente i contributi di ogni termine:

\bullet \quad \frac { \partial \left| { Z }_{ X } \right| }{ \partial { V }_{ Zmax } } =\frac { \partial }{ \partial { V }_{ Zmax } } \left[ \frac { { V }_{ Zmax } }{ { V }_{ Rmax } } \cdot { R }_{ C } \right] =\frac { { R }_{ C } }{ { V }_{ Rmax } } =161,29\\ \bullet \quad U({ V }_{ Zmax })=\quad \pm (3\%\quad of\quad reading+0,1div+1mV)=0,407\\ \bullet \quad \frac { \partial \left| { Z }_{ X } \right| }{ \partial { V }_{ Rmax } } =\frac { \partial }{ \partial { V }_{ Rmax } } \left[ \frac { { V }_{ Zmax } }{ { V }_{ Rmax } } \cdot { R }_{ C } \right] =-\frac { { V }_{ Zmax } }{ { { V }_{ Rmax } }^{ 2 } } \cdot { R }_{ C }=-3511,96\\ \bullet \quad U({ V }_{ Rmax })=\quad \pm (3\%\quad of\quad reading+0,1div+1mV)=0,0207\\ \bullet \quad \frac { \partial \left| { Z }_{ X } \right| }{ \partial { R }_{ C } } =\frac { \partial }{ \partial { R }_{ C } } \left[ \frac { { V }_{ Zmax } }{ { V }_{ Rmax } } \cdot { R }_{ C } \right] =\frac { { V }_{ Zmax } }{ { V }_{ Rmax } } =21,77\\ \bullet \quad U({ R }_{ C })=\quad 0,1\%\quad of\quad reading+4digit=0,10177+0,04=0,14

Da cui:

U(\left| { Z }_{ X } \right| )=\pm 98\\ \\ { \sigma }_{ { Z }_{ X } }=\pm \frac { U(\left| { Z }_{ X } \right| ) }{ \sqrt { 3 } } =\pm \frac { 98 }{ \sqrt { 3 } } =\pm 56,58

Ottenendo infine:

\left| { Z }_{ X } \right| =2215,96\pm 56,58

Ricavata l’espressione del modulo dell’impedenza, è possibile trovarne parte reale e immaginaria.
Si misura, tramite l’oscilloscopio, la differenza di fase tra la correte 𝐼𝑍 e la tensione 𝑉𝑍.
Siccome la corrente è la stessa che passa per 𝑅𝐶 ed è costante, si ha che 𝑉𝑅𝐶 è proporzionale a 𝐼𝑍 e presenta la stessa sua fase.
Per ricavare la differenza di fase si valuta il Δt sul display dell’oscilloscopio, ovvero l’intervallo di tempo che intercorre tra il passaggio dei due segnali da zero.
Imponendo una semplice proporzione si ha l’espressione dello sfasamento:

\frac { \Delta t }{ T } =\frac { \varphi }{ 2\pi }

Ora, per definizione:

{ R }_{ X }=Re\left\{ { Z }_{ X } \right\} =\left| { Z }_{ X } \right| \cos { \varphi } \\ \\ { X }_{ X }=Im\left\{ { Z }_{ X } \right\} =\left| { Z }_{ X } \right| \sin { \varphi }

𝜑 rappresenta quindi lo sfasamento tra la tensione e la corrente, come precedentemente espresso:

\varphi =2\pi f\Delta t=2\pi \frac { \Delta t }{ T }

dove:

f≝\frac { 1 }{ T } =50 Hz

è la frequenza della corrente alternata fornita dalle prese elettriche, con periodo

T=\frac { 1 }{ f } =20ms

mentre Δ𝑡, si ricorda, è l’intervallo di tempo che intercorre tra il passaggio dei due segnali da zero.
Tutte le misure effettuate risentono di incertezza, esprimibile come

\frac { fondoscala }{ 10 } \cdot \frac { 1 }{ \sqrt { 3 } }

Per le misure effettuate sul Δ𝑡, sì è utilizzata la convenzione degli utilizzatori: è stato quindi invertito il verso del segnale visualizzato sullo schermo dell’oscilloscopio, successivamente si è letta la misura con il segno. Analizzando i segnali, è stato possibile constatare che 𝑉𝑍𝑚𝑎𝑥 è in anticipo rispetto a 𝑉𝑅𝐶, quindi l’impedenza ha parte immaginaria negativa, confermando dunque la sua natura capacitiva.
Si è quindi ottenuto:

\Delta t\cong 1ms

Ricavati questi ultimi dati, è possibile calcolare il valore di 𝑅𝑥 e 𝑋𝑥.

{ R }_{ X }=Re\left\{ { Z }_{ X } \right\} =\left| { Z }_{ X } \right| \cos { \varphi } = =\frac { { V }_{ Zmax } }{ { V }_{ Rmax } } \cdot R_{ C }\cdot \cos { \left( 2\pi \frac { \Delta t }{ T } \right) } = =\frac { 13,5 }{ 0,62 } \cdot 101,77\cdot \cos { \left( 2\pi \frac { { 10 }^{ -3 } }{ 20\cdot { 10 }^{ -3 } } \right) } = =2107,5\Omega ***** { X }_{ X }=Im\left\{ { Z }_{ X } \right\} =\left| { Z }_{ X } \right| \sin { \varphi } = =\frac { { V }_{ Zmax } }{ { V }_{ Rmax } } \cdot R_{ C }\cdot \sin { \left( 2\pi \frac { \Delta t }{ T } \right) } = =\frac { 13,5 }{ 0,62 } \cdot 101,77\cdot \sin { \left( 2\pi \frac { { 10 }^{ -3 } }{ 20\cdot { 10 }^{ -3 } } \right) } = =-684,77\Omega ***** U(R_{ X })=\pm 332,5 { \sigma }_{ { R }_{ X } }=\pm \frac { U(R_{ X }) }{ \sqrt { 3 } } =\pm \frac { 332,5 }{ \sqrt { 3 } } =\pm 186,19 ***** U(X_{ X })=\pm 414,8 { \sigma }_{ { X }_{ X } }=\pm \frac { U(X_{ X }) }{ \sqrt { 3 } } =\pm \frac { 414,8 }{ \sqrt { 3 } } =\pm 239,5

Concludendo, il valore comprensivo di incertezze dell’impedenza incognita risulta essere:

Z_{ X }=R_{ X }\pm jX_{ X }=\left( 2107,5±186,19 \right) -j\left( 684,77±239,5 \right)