In questo articolo si andrà a descrivere brevemente alcuni aspetti legati al filtraggio di segnali, in particolare discreti, introducendo le principali tipologie di filtro FIR e IIR.
In molte applicazioni e contesti è utile effettuare operazioni di filtraggio. Ciò può essere fatto realizzando circuiti elettrici progettati in diversi modi a seconda dei requisiti. Ad esempio, un filtro passa-basso passivo può essere ricreato con un paio di componenti, in modo semplice ed economico.
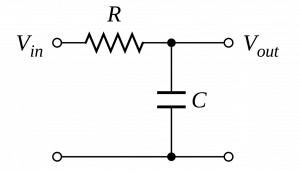
Esistono alcune condizioni però in cui l’utilizzo di questo approccio analogico risulta poco efficace, per diversi fattori.
L’utilizzo di filtri digitali riesce ad essere a volte più economico e immediato rispetto ai filtri analogici. I filtri digitali permettono di progettare e ottenere funzioni di trasferimento di difficile realizzazione nel campo analogico. Inoltre, per elaborare segnali discreti (non continui) si è obbligati a usare filtri di tipo digitale. I filtri digitali possono essere modificati al volo (on the fly) via software e senza modificare l’hardware.
Le principali tipologie di filtri digitali si suddividono in:
- FIR: sistema LTI (Lineare Tempo Invariante, o Stazionario) causale con risposta finita all’impulso;
- IIR: sottoclasse di sistemi LTI causali con risposta anche infinita all’impulso.
È preferibile scegliere un filtro FIR se le specifiche richiedono un filtraggio a fase lineare, con un certo grado di stabilità. Viceversa, i filtri IIR introducono una distorsione in fase, richiedendo però un minor numero di parametri da settare e minor complessità computazionale. Da questi filtri è possibile ottenere una migliore risposta in termini di banda e attenuazione.
Al fine di progettare un filtro esistono diverse tecniche. Per IIR, le principali sono:
- Invarianza Impulsiva, campionando la risposta a tempo continuo;
- Trasformazione Bilineare, basata sulla relazione tra i piani complessi in s (dominio di Laplace) e in z (dominio Zeta).
Per FIR, le principali sono:
- Finestre temporali, effettuando un’approssimazione per troncamento.
Negli articoli successivi, si entrerà nel dettaglio di queste tecniche, definendo i formalismi matematici e tirando alcune interessanti considerazioni.
Fonti:
[Luise, M., & Vitetta, G. M. (2009). Teoria dei segnali (3ª ed.). McGraw-Hill Companies.]
Per questo articolo è tutto.
Per dubbi, errori o semplicemente ringraziamenti, puoi contattarci attraverso i nostri contatti social.
Puoi seguirci sul sito: www.antima.it
su Instagram: https://www.instagram.com/antima.it/
su Facebook: https://www.facebook.com/Antima.it/