Comportamento non ideale dei componenti – Il resistore

Obiettivo di questo articolo è quello di analizzare e valutare qualitativamente gli effetti parassiti, legati alle terminazioni di un resistore, al variare della frequenza.

Nel precedente articolo introduttivo, si è studiato il problema in generale e  si è chiarito l’approccio per analizzarlo. Ci si propone ora di valutare nello specifico il caso di studio di un resistore generico.

Si vuole caratterizzare il suo comportamento non ideale.
Come descritto precedentemente per la generica impedenza Z, si può modellare un circuito che tiene conto dei fenomeni alle terminazioni, come in figura.

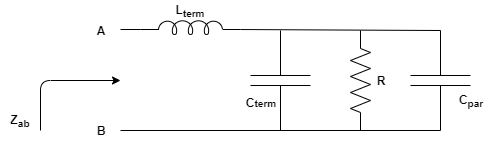
In particolare, oltre agli effetti sulle terminazioni, è stato inserito un capacitore Cpar in parallelo al resistore. Questo capacitore tiene conto dell’accumulo di cariche sull’involucro del resistore (in genere, dell’ordine di 1 pF). Risolvendo il circuito, si ha:

{ Z }_{ ab }=\quad j\omega { L }_{ term }+\left( \frac { \frac { R }{ j\omega { C }_{ eq } }  }{ R+\frac { 1 }{ j\omega { C }_{ eq } }  }  \right) 

Dove

{ C }_{ eq }={ C }_{ term }+{ C }_{ par }

Manipolando l’espressione di 𝑍𝑎𝑏 si ottiene

{ Z }_{ ab }=j\omega { L }_{ term }+\left( \frac { R }{ 1+j\omega R{ C }_{ eq } }  \right) 

Manipolando anche il circuito, avremo:

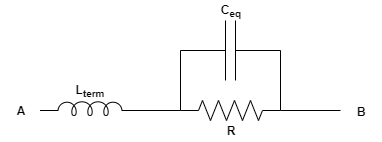
Dall’espressione di 𝑍𝑎𝑏 e dal circuito equivalente risulta fin da subito chiaro che il valore complessivo sia dato dal contributo del termine resistivo, induttivo e capacitivo. Inoltre, l’espressione indica chiaramente che 𝑍𝑎𝑏 sia dipendente dalla frequenza di lavoro. Si procede dunque con l’analisi del modello.

Analisi del modello

Dall’espressione di 𝑍𝑎𝑏, è possibile analizzarne il comportamento asintotico.

\begin{cases} \omega \rightarrow 0\quad \quad \Rightarrow \quad \quad { Z }_{ ab }\cong R \\ \omega \rightarrow \infty \quad \quad \Rightarrow \quad \quad { Z }_{ ab }\cong \infty  \end{cases}

Da cui si ricavano i rispettivi modelli semplificati del circuito.

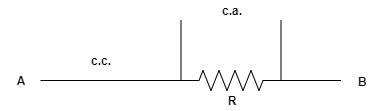
In questo modo sono stati definiti gli andamenti asintotici a frequenze nulle e infinite. L’impedenza complessiva 𝑍𝑎𝑏 sarà puramente resistiva con valore pari a R per frequenze basse, aumentando all’aumentare delle frequenze.
Per caratterizzare totalmente il comportamento del resistore, risulta necessario valutarne l’andamento nei valori intermedi di frequenze. Per valori intermedi di frequenza, o pulsazione ω, la reattanza induttiva e capacitiva offerta dagli effetti parassiti diventano paragonabili al resistore.

Esisterà dunque un valore di pulsazione ω = ω1 (o di frequenza 𝑓1) per cui:

R\cong \left| \frac { 1 }{ j{ \omega  }_{ 1 }{ C }_{ eq } }  \right| \rightarrow R=\frac { 1 }{ { \omega  }_{ 1 }{ C }_{ eq } } \rightarrow { \omega  }_{ 1 }=\frac { 1 }{ R{ C }_{ eq } } \rightarrow { f }_{ 1 }=\frac { 1 }{ 2\pi R{ C }_{ eq } } 

𝑓1 è la frequenza per la quale il valore di reattanza capacitiva è paragonabile al valore di resistenza del resistore. Nell’intorno di questa frequenza non sarà possibile trascurare l’effetto capacitivo.
Inoltre, si avrà:

{ Z }_{ ab }=R\quad //\quad { C }_{ eq }

Per cui si dovrà tener conto di entrambi i contributi di R e 𝐶𝑒𝑞.

Per valori di ω > ω1, l’effetto capacitivo prevarrà su quello resistivo, per cui:

\omega >{ \omega  }_{ 1 }\rightarrow { Z }_{ ab }\cong { C }_{ eq }=\frac { 1 }{ j\omega { C }_{ eq } } 

Ciò è descrivibile elettricamente in quanto R è costante mentre il valore offerto dalla reattanza capacitiva decresce all’aumentare della frequenza. Nel parallelo tra i due prevale il percorso a bassa impedenza.
In modo analogo, esisterà un valore di pulsazione ω = ω2 (o di frequenza 𝑓2) tale che la reattanza capacitiva sia uguale a quella induttiva. Questa è la condizione per cui si abbia il fenomeno di risonanza. Per cui:

\left| j{ \omega  }_{ 2 }{ L }_{ term } \right| \cong \left| \frac { 1 }{ j{ \omega  }_{ 2 }{ C }_{ eq } }  \right| 

{ \omega  }_{ 2 }{ L }_{ term }=\frac { 1 }{ { \omega  }_{ 2 }{ C }_{ eq } } \rightarrow { \omega  }_{ 2 }=\sqrt { \frac { 1 }{ { L }_{ term }{ C }_{ eq } }  } \rightarrow { f }_{ 2 }=\frac { 1 }{ 2\pi \sqrt { { L }_{ term }{ C }_{ eq } }  } 

In condizione di risonanza, si avrà:

{ Z }_{ ab }=j{ \omega  }_{ 2 }{ L }_{ term }+\frac { 1 }{ j{ \omega  }_{ 2 }{ C }_{ eq } } \cong 0

Infine, per valori di ω > ω2, l’effetto induttivo prevarrà su quello capacitivo, per cui:

{ Z }_{ ab }=j{ \omega  }_{ 2 }{ L }_{ term }

Riepilogando:

\begin{cases} \omega \rightarrow 0\quad \quad \qquad \Rightarrow { Z }_{ ab }\cong R \\ { \omega  }_{ 1 }<\omega <{ \omega  }_{ 2 }\quad \Rightarrow { Z }_{ ab }\cong \frac { 1 }{ j\omega { C }_{ eq } }  \\ \omega >{ \omega  }_{ 2 }\qquad \quad \quad \Rightarrow { Z }_{ ab }\cong j\omega { L }_{ term } \end{cases}

Simulazione Matlab

Come visto nel paragrafo precedente, il resistore mantiene il suo comportamento ottimale per frequenze relativamente basse, o comunque minori di ω1. È questo il range a cui bisogna far lavorare il resistore per non incorrere in fenomeni indesiderati.
Il resistore può assumere però valori di resistenza bassi o elevati, in funzione dello specifico utilizzo che se ne fa all’interno di un progetto. Ciò influenzerà non solo il comportamento alle alte frequenze, ma anche il range di frequenze ottimali a cui può lavorare. Si utilizza quindi il software matematico Matlab per valutare i diversi casi, considerando valori di resistenza e effetti alle terminazioni realistici. Inoltre, saranno confrontate tecnologie costruttive differenti che influenzano il valore tipico degli effetti alle terminazioni. I valori tipici degli effetti parassiti sono riassunti in questa tabella.

Resistore a filo

Di seguito, viene riportato il codice Matlab relativo all’analisi e al confronto tra il comportamento di un resistore a filo di valore 1kΩ rispetto a uno di 25 Ω. Nel confronto è stato tenuto conto sia dell’andamento reale, ottenuto dall’espressione di 𝑍𝑎𝑏 al variare della frequenza, sia quello asintotico ricavato nei range di frequenze di particolare interesse, precedentemente ricavati.

Per il resistore da 1kΩ, si definiscono inizialmente le variabili, con particolare attenzione al valore degli effetti alle terminazioni e al range di frequenze indicate nella traccia. Si riportano le formule ricavate nel paragrafo precedente, con il valore di 𝑍𝑎𝑏 espresso anche in decibel: i grafici riportati saranno espressi in scala logaritmica.
Vengono calcolate le frequenze 𝑓1 e 𝑓2, in modo da suddividere il vettore di frequenze complessivo in sottovettori, con lo scopo di associare ad ognuno di essi uno specifico andamento e comportamento (resistivo, capacitivo o induttivo).
Con una serie di plot e accorgimenti grafici si visualizza infine il risultato.

Con lo stesso metodo si realizza il secondo grafico, relativo al resistore da 25 Ω. Per ottenere un confronto più leggibile e immediato, si è utilizzata la funzione subplot() nativa di Matlab, grazie alla quale è possibile visualizzare più grafici allineati nella stessa finestra.
Sono stati scelti come valori Lterm = 100nH e Cp = 0,75pF.

A questo link il codice Matlab commentato.

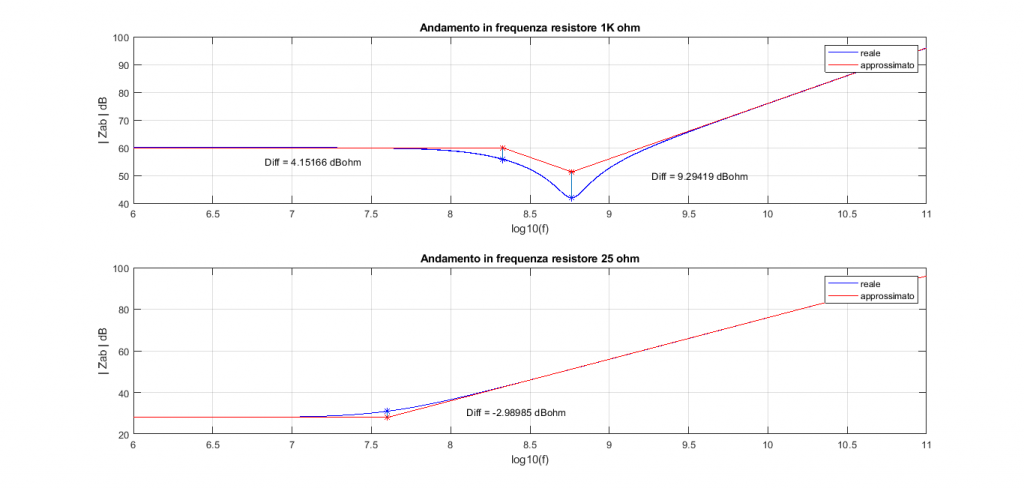
Di seguito i grafici ottenuti per il confronto tra due resistori a filo di diverso valore nominale:

Resistore SMD

Di seguito, viene riportato il codice Matlab relativo all’analisi e al confronto tra il comportamento di un resistore SMD di valore 1kΩ rispetto a uno di 25 Ω. Nel confronto è stato tenuto conto sia dell’andamento reale, ottenuto dall’espressione di 𝑍𝑎𝑏 al variare della frequenza, sia quello asintotico ricavato nei range di frequenze di particolare interesse, precedentemente ricavati.

Il codice è analogo al caso precedente, considerando però valori degli effetti alle terminazioni tipici della tecnologia SMD.

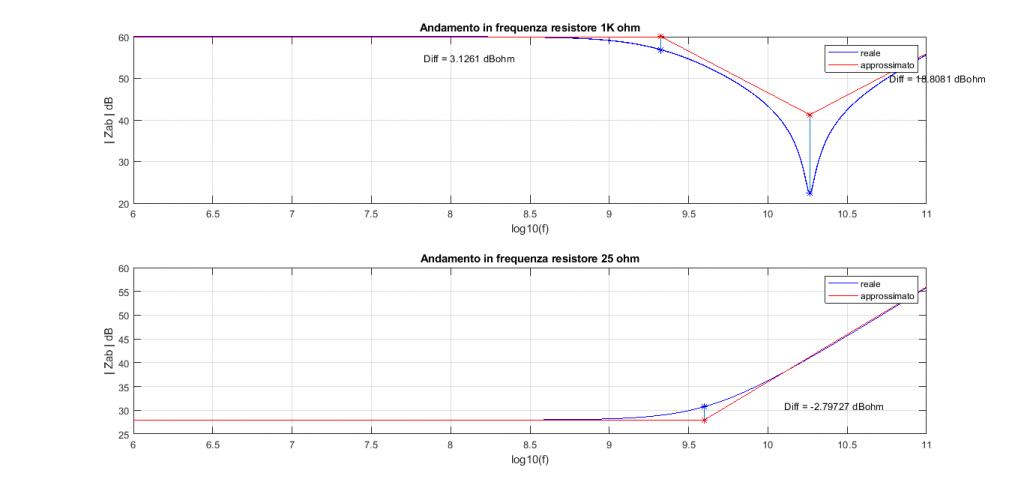
Di seguito i grafici ottenuti per il confronto tra due resistori SMD di diverso valore nominale:

Considerazioni

Dai grafici ottenuti è possibile fare alcune considerazioni sul comportamento dei resistori. In particolare, è possibile confrontare l’andamento tra diversi valori di resistenza, ma anche tra le diverse tecnologie.

Nel grafico in figura 10 si ha il confronto tra i due resistori a filo di diverso valore.
Nel caso di resistore da 1k è possibile apprezzare gli andamenti studiati nei paragrafi precedenti. Fino alla frequenza 𝑓1 si ha il comportamento resistivo. Da 𝑓1 a 𝑓2 è possibile notare il comportamento capacitivo, mentre per frequenze superiori si ha il comportamento induttivo. Le frequenze di interesse per questo caso sono:

{ f }_{ 1 }=2,12\cdot { 10 }^{ 8 }Hz=212MHz\\ { f }_{ 2 }=5,81\cdot { 10 }^{ 8 }Hz=581MHz

Ciò significa che il range di frequenze ottimali per questo resistore è fino a 212 𝑀𝐻𝑧.

Nel caso di resistore da 25 Ω è possibile apprezzare gli andamenti studiati nei paragrafi precedenti. Fino alla frequenza 𝑓1 si ha il comportamento resistivo, oltre si ha il comportamento induttivo. Le frequenze di interesse per questo caso sono:

{ f }_{ 1 }=39,8\cdot { 10 }^{ 6 }Hz=39,8MHz

Ciò significa che il range di frequenze ottimali per questo resistore è fino a 39,8 𝑀𝐻𝑧.
Sia graficamente che analiticamente è possibile notare che il resistore a valore più basso ha una banda di frequenze ottimale più ristretta.

Un’ulteriore osservazione riguarda il comportamento capacitivo non presente nel caso di resistore a basso valore. Ciò è spiegabile in quanto l’effetto induttivo si innesca a frequenze minori, quindi prima, non permettendo all’effetto capacitivo di entrare in gioco.

Tutte queste considerazioni possono essere fatte nel caso di tecnologia SMD, i cui grafici sono visibili in figura.
Di particolare interesse però è confrontare le frequenze di interesse tra le due tecnologie. Infatti, nel caso SMD con resistore da 1k, si ha

{ f }_{ 1 }=2,12\cdot { 10 }^{ 9 }Hz=2,12GHz\\ { f }_{ 2 }=18,37\cdot { 10 }^{ 9 }Hz=18,37GHz

Mentre nel caso di resistore da 25 Ω con tecnologia SMD si ha:

{ f }_{ 1 }=3,98\cdot { 10 }^{ 9 }Hz=3,98GHz

Da notare che tutte le frequenze di interesse siano traslate di molto con i resistori SMD, confermando le caratteristiche e i risultati migliori ottenibili con questa tecnologia.
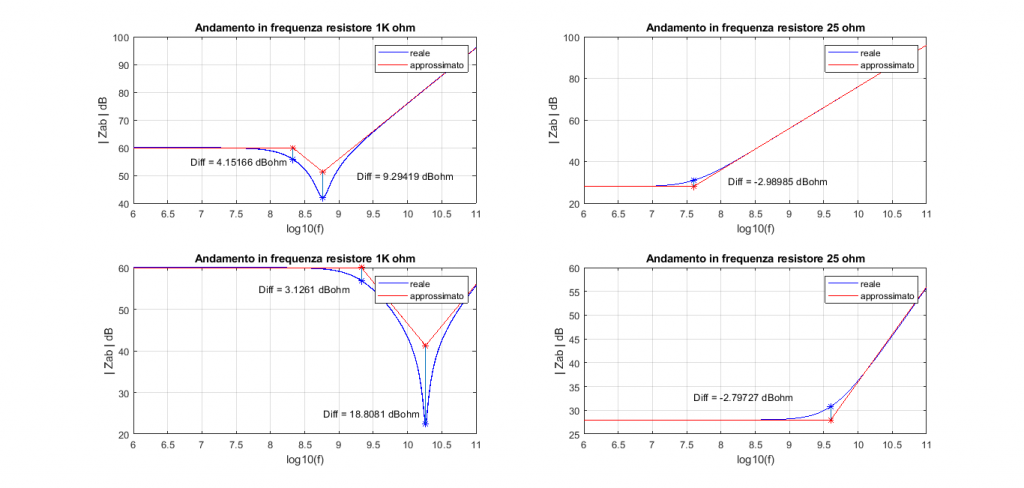
Infine, nella seguente figura, i grafici ottenuti a confronto.

Per questo articolo è tutto.

Per dubbi, errori o semplicemente ringraziamenti, puoi contattarci attraverso i nostri contatti social.