in Elettronica |

Tecniche di progettazione IIR: Trasformazione bilineare

In questo articolo si andrà a illustrare un’altra tecnica per la progettazione di filtri digitali IIR, ovvero il metodo della trasformazione bilineare.

Nei precedenti articoli abbiamo introdotto i concetti di filtraggio digitale, definendo poi una prima tecnica, ovvero la tecnica della varianza impulsiva. Ora tratteremo un approccio differente al problema, grazie al quale sarà possibile estendere le possibilità di filtraggio viste con la precedente tecnica.

Data una funzione di trasferimento Ha(s) razionale fratta:

{ H }_{ a }(s)=\frac { 1 }{ 1+s\tau } \quad con\quad \tau =RC

Si ricava l’equazione differenziale:

{ H }_{ a }(s)=\frac { Y(s) }{ X(s) } \quad \rightarrow \quad \frac { Y(s) }{ { H }_{ a }(s) } =X(s)\quad \rightarrow \quad Y(s)\cdot \left( 1+s\tau \right) =X(s)

da cui:

y(t)+\tau \frac { dy(t) }{ dt } =x(t)

Integrando ambo i membri:

\int _{ { t }_{ 0 } }^{ t }{ y(\alpha )d\alpha +\tau \left[ y(t)-y({ t }_{ 0 }) \right] } =\int _{ { t }_{ 0 } }^{ t }{ x(\alpha ) } d\alpha

Valutiamo questa relazione tra:

\\ { t }_{ 0 }=(n-1)T\quad \quad e\quad \quad t=nT

Con T=intervallo di campionamento. Otteniamo:

\int _{ (n-1)T }^{ nT }{ y(\alpha )d\alpha +\tau \left[ y(nT)-y((n-1)T) \right] } =\int _{ (n-1)T }^{ nT }{ x(\alpha ) } d\alpha

Il nostro obiettivo è ottenere una relazione nel tempo discreto simile a quella ottenuta per i segnali analogici. A tal fine, si approssimano gli integrali con una formula numerica. Ad esempio, l’integrale al secondo membro può essere approssimato con la regola del trapezio.

Area\quad sottesa\quad al\quad grafico\quad \cong \quad Area\quad trapezio
\int _{ (n-1)T }^{ nT }{ x(\alpha ) } d\alpha \quad \cong \quad \frac { T }{ 2 } \left[ x(nT)+x((n-1)T) \right]

Applicando questa formula ad entrambi gli integrali si ottiene:

\frac { T }{ 2 } \left[ y(nT)+y((n-1)T) \right] +\tau \left[ y(nT)-y((n-1)T) \right] \cong \frac { T }{ 2 } \left[ x(nT)+x((n-1)T) \right]
\\ Y[n]=Y[nT]\quad ;\quad X[n]=X[nT]

Sostituendo, dopo alcuni passaggi, si ottiene:

Y[n]\cong \frac { \tau -\frac { T }{ 2 } }{ \tau +\frac { T }{ 2 } } Y[n-1]\quad +\quad \frac { \frac { T }{ 2 } }{ \tau +\frac { T }{ 2 } } \left( X[n]+X[n-1] \right)

che rappresenta l’equazione alle differenze del sistema tempo discreto cercato. Applicando la trasformata z:

H(z)=\frac { Y(z) }{ X(z) } =\frac { \sum _{ k=0 }^{ M }{ { b }_{ k }{ \cdot z }^{ -k } } }{ 1+\sum _{ m=1 }^{ N }{ { a }_{ m }{ \cdot z }^{ -m } } } =\\ \\ \frac { \frac { \frac { T }{ 2 } }{ \tau +\frac { T }{ 2 } } (1+{ z }^{ -1 }) }{ 1-\frac { \tau -\frac { T }{ 2 } }{ \tau +\frac { T }{ 2 } } { z }^{ -1 } } =\frac { 1 }{ 1+\left( \frac { 2 }{ T } \right) \frac { 1-{ z }^{ -1 } }{ 1+{ z }^{ -1 } } \tau }

Confrontando l’espressione ottenuta con quella analogica, si ha:

H(z)={ H }_{ a }\left( \frac { 2 }{ T } \frac { 1-{ z }^{ -1 } }{ 1+{ z }^{ -1 } } \right)

da cui possiamo ricavare H(z) da Ha(s). La relazione:

s=\frac { 2 }{ T } \frac { 1-{ z }^{ -1 } }{ 1+{ z }^{ -1 } }

crea una trasformazione tra i piani complessi s e z, ovvero una trasformazione bilineare. Si ricava inoltre la formula inversa:

z=\frac { 1+s\frac { T }{ 2 } }{ 1-s\frac { T }{ 2 } }

anch’essa bilineare. Se poniamo s=σ+jω si ottiene:

\left| z \right| =\sqrt { \frac { { \left( 1+\sigma \frac { T }{ 2 } \right) }^{ 2 }+{ \left( \omega \frac { T }{ 2 } \right) }^{ 2 } }{ { \left( 1-\sigma \frac { T }{ 2 } \right) }^{ 2 }+{ \left( \omega \frac { T }{ 2 } \right) }^{ 2 } } }

da cui si ricavano informazioni sulla stabilità del sistema.
Supponiamo Ha(s) stabile (parte reale di spi minore di zero). Ricaviamo zpi dalla formula precedente. Se spi ha parte reale negativa (σ<0), allora il modulo |zpi|ed il sistema tempo discreto è stabile.

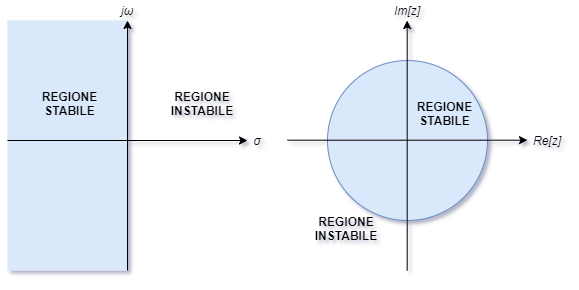
La risposta in frequenza H(f) del sistema tempo discreto ottenuta dalla trasformazione bilineare si ottiene valutando la funzione di trasferimento sui punti della circonferenza di raggio unitario |z|=1.

\\ \overline { H } (f)=H\left( { e }^{ j2\pi fT } \right)
\\ z={ e }^{ j2\pi fT }

si ottiene:

s=j\frac { 2 }{ T } \tan { \left( \pi fT \right) }

Indicando con fa la frequenza relativa al piano s del sistema a tempo continuo, si ha:

\sigma +j2\pi { f }_{ a }=j\frac { 2 }{ T } \tan { \left( \pi fT \right) } \\ 2\pi { f }_{ a }=\frac { 2 }{ T } \tan { \left( \pi fT \right) } \\ { f }_{ a }=\frac { 1 }{ \pi T } \tan { \left( \pi fT \right) }

quindi:

\overline { H } (f)=H\left( \frac { 1 }{ \pi T } \tan { \left( \pi fT \right) } \right)

In termini di caratteristiche in frequenza (selettività), vi è un legame tra filtro ottenuto tramite trasformazione bilineare e quello del prototipo analogico.

Tra gli aspetti di rilievo di questa tecnica, si può dire che:

  • La trasformazione bilineare, rispetto all’invarianza impulsiva, non da luogo all’aliasing. Si possono usare filtri a banda illimitata, come passa-alto e elimina-banda.
  • Compressione/distorsione della risposta in frequenza (warping). Per preservare la risposta in frequenza ad una frequenza, si applica una predistorsione (prewarping). 

 

 

Fonti:

  • [Luise, M., & Vitetta, G. M. (2009). Teoria dei segnali (3ª ed.). McGraw-Hill Companies.]

 

⇐ Tecniche di progettazione IIR: Varianza Impulsiva – Ulteriori considerazioni

Per questo articolo è tutto.

Per dubbi, errori o semplicemente ringraziamenti, puoi contattarci attraverso i nostri contatti social.

Puoi seguirci sul sito: www.antima.it
su Instagram: https://www.instagram.com/antima.it/
su Facebook: https://www.facebook.com/Antima.it/

Pubblicato

Scrivi un commento

Commento