In questo articolo si descriverà il metodo di misura dell’angolo di fase di segnali sinusoidali isofrequenziali attraverso il metodo dell’ellisse (figure di Lissajous).
Strumentazione
- Generatore di segnale Tektronix CFCX253 (Serial Number: CFG-253TN60109);
- Oscilloscopio Tektronix TDS 210 (Serial Number: B122711);
- Cavi di collegamento con connettore a banana;
- Sonda con connettore BNC.
Componenti utilizzati
- Resistenza R;
- Condensatore C (47nF).
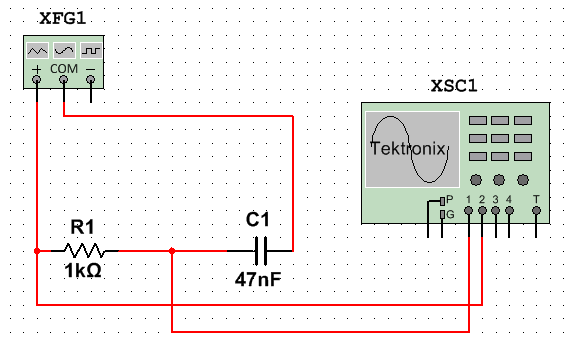
Circuito
Considerazioni preliminari
Una figura di Lissajous è il grafico di una curva data dal sistema di equazioni parametriche:
Dove Ax e AY sono le ampiezze, ωx e ωY sono le pulsazioni e φx e φY sono le fasi di due moti oscillatori ortogonali.
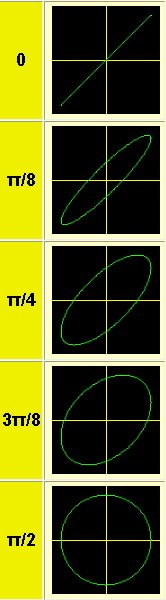
L’aspetto di queste figure è molto sensibile al rapporto ωx ⁄ ωY tra le due pulsazioni, ma anche agli altri parametri.
Un approccio allo studio può esser quello di valutare queste curve modificando un parametro alla volta:
1. Ax = AY ; ωx = ωY
Con queste condizioni si ottengono le principali figure. Nella misura dell’angolo di fase di segnali sinusoidali isofrequenziali è evidente come queste curve diano un’idea generale delle caratteristiche dei segnali, ma possono essere, come si vedrà, un forte strumento in tal senso.
2. ωx = ωY
3. ωx / ωY ∈ Q
Nel caso in cui il rapporto tra le pulsazioni sia un numero razionale Q, si ottengono delle figure più complicate, compresa la parabola, ma in ogni caso periodiche, intendendo con questo termine il fatto che dopo un certo tempo il punto del piano (x, y) “ritorna sui suoi passi”, cioè ridisegna esattamente la stessa curva e così di seguito con lo scorrere del tempo.
4. ωx / ωY ∉ Q
Nel caso in cui il rapporto tra le pulsazioni sia un numero irrazionale, viene a cadere la periodicità della figura.
La misura
Si procede inizialmente alla realizzazione del circuito, collegando il generatore di funzioni, tramite i cavi, all’impedenza RC serie.
All’uscita del generatore di funzioni (boccola MAIN) si collega l’adattatore BNC rosso/nero. Alla boccola nera dell’adattatore si collega il terminale negativo del condensatore C, alla boccola rossa invece l’estremità della resistenza R.
La misura prevede l’utilizzo dell’oscilloscopio: tramite apposita sonda BNC si collega l’estremità nera alla massa del circuito e l’uncino (parte calda) all’altra estremità dell’impedenza.
Ultimati i collegamenti, si accendono gli strumenti e si attende affinché il circuito vada a regime.
Si imposta sul generatore di funzioni una frequenza pari a 1 kHz e si analizzerà sull’oscilloscopio le sinusoidi relative all’impedenza complessiva e al solo condensatore. Particolare attenzione viene posta nel porre su entrambi i canali lo stesso valore di VOLTS/DIV, posizionando i due segnali sovrapponendoli sullo stesso asse orizzontale.
Per poter visualizzare le curve di Lissajous nel caso in esame, si rende necessario visualizzare il relativo grafico parametrizzando tali segnali: l’oscilloscopio presenta esattamente la funzione necessaria, basterà premere il pulsante DISPLAY in modo da poter visualizzare tutti i tool grafici presenti e cambiare formato da YT (ampiezza in funzione del tempo) a XY. Con questi comandi sarà possibile visualizzare le curve di Lissajous.
Per una maggiore accuratezza sulle misure e calcoli che si faranno sul grafico ottenuto, si “centra” quanto più possibile la figura tramite le relative manopole di posizione.
Il grafico ottenuto dipenderà fortemente, come visto precedentemente, dai legami che intercorrono tra i segnali prelevati. Sarà necessario procedere matematicamente al fine di determinare con accuratezza la differenza di fare, obiettivo di questa misura.
I due segnali producono degli spostamenti della traccia sullo schermo dell’oscilloscopio esprimibile con le seguenti relazioni generiche:
Nel caso in esame i segnali sono isofrequenziali dunque ωx = ωY = ⍵.
È possibile ottenere una rappresentazione parametrica di un segnale rispetto all’altro scrivendo
e
da cui
Elevando al quadrato primo e secondo membro:
Sviluppando
Poiché vale l’identità:
sostituendo:
Per la stessa identità di prima, si ha l’equazione dell’ellisse:
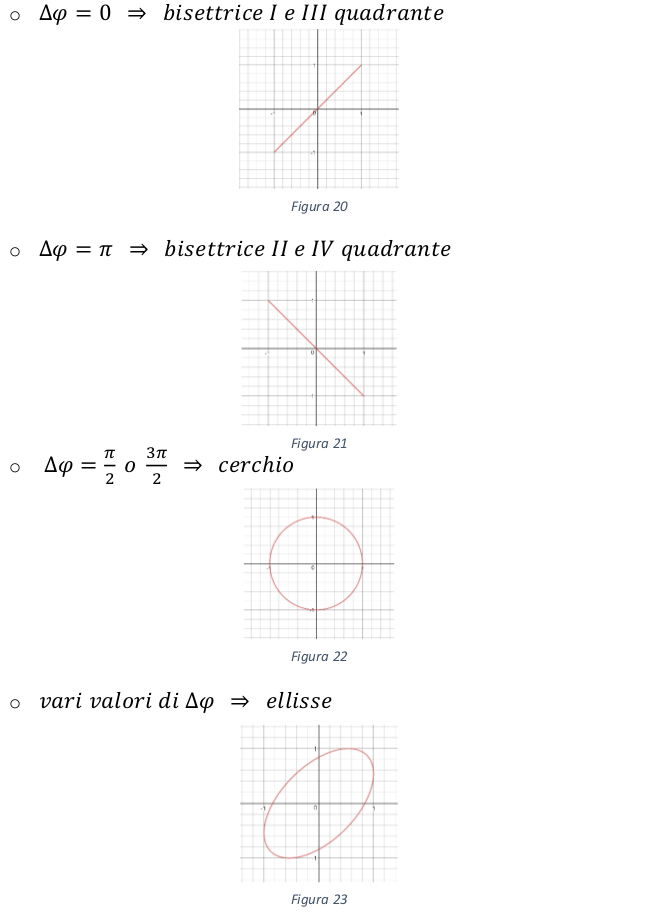
Osserviamo che l’ellisse diventa una circonferenza se i segnali hanno la stessa ampiezza ( Ax = Ay )e sono sfasati di π/2 o 3π/2. L’ellisse diventa una retta quando lo sfasamento è ∆φ = 0 oppure π.
La traccia dell’ellisse sullo schermo non cambia orientamento variando la fase al valore positivo di ∆φ al valore negativo di −∆φ . Ne consegue che nella misura dell’angolo di sfasamento con il metodo dell’ellisse si ha un’indeterminazione sul segno dello sfasamento.
Per determinare l’angolo di sfasamento si procede come da figura: si misura la massima estensione verticale dell’ellisse AB e la larghezza dell’ellisse per x=0 CD.
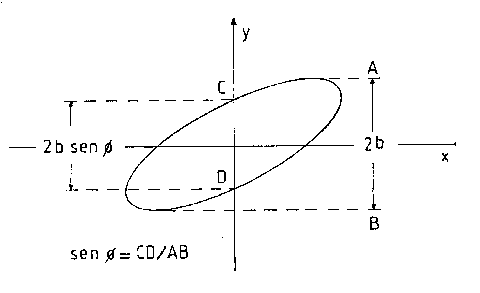
In tal modo si giunge alla conclusione che
Oltre all’indeterminazione del segno, il calcolo di |∆φ| fornisce sempre valori compresi tra 0° e 90°, anche quando in effetti lo sfasamento ha un modulo compreso tra 90° e 180°.
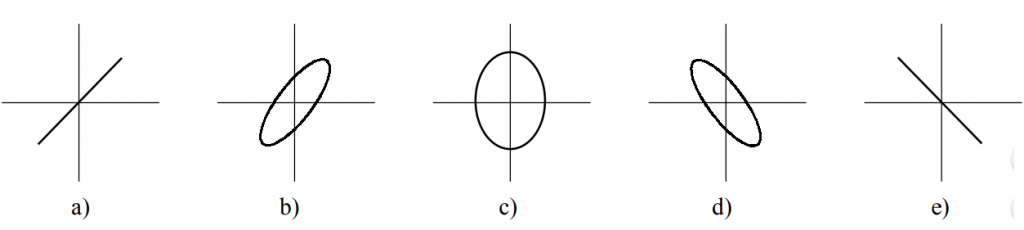
Dal tipo di figura visualizzata è possibile però determinare se sia necessario o meno aggiungere 90° al valore calcolato. Con riferimento alla figura si hanno i seguenti casi:
Siccome è possibile fissare il valore di A arbitrariamente, è opportuno, per avere la massima precisione nella misura, fissare A al massimo valore.
Si nota inoltre che è sufficiente misurare A e B in divisioni in quanto tali quantità vanno a costituire un rapporto e ciò rende superflua la moltiplicazione di entrambe le grandezze per lo stesso fattore di scala.
È possibile verificare che per i valori di frequenza prossimi alla risonanza non è possibile risalire ai valori di AB e CD poiché l’ellisse risulta degenere al punto da assomigliare ad una retta.
Dalle misure effettuate in laboratorio si è ottenuto:
con il seguente grafico:
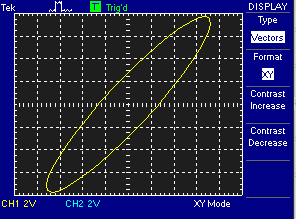
Per cui si ha:
Che ricade nel caso b) precedentemente studiato.
Per l’incertezza, si ha:
Ottenendo:
E infine: